Introduction
Consider conducting research to determine whether a newly introduced medication effectively lowers blood pressure? You administer the drug to a cohort of patients suffering from the targeted condition, and compare their outcomes with those of a control group that receives an inert placebo treatment. It appears to significantly lower blood pressure, whereas in reality, it does not. The flawed denial of the null hypothesis’s implication that the medication exerts no influence is a type I error. If the medication indeed reduces blood pressure but your study is unable to capture this effect due to flawed methodology or data inconsistency? As a direct result, it becomes evident that the drug is indeed ineffective, thereby committing the error of failing to reject a false null hypothesis – a Type II mistake.
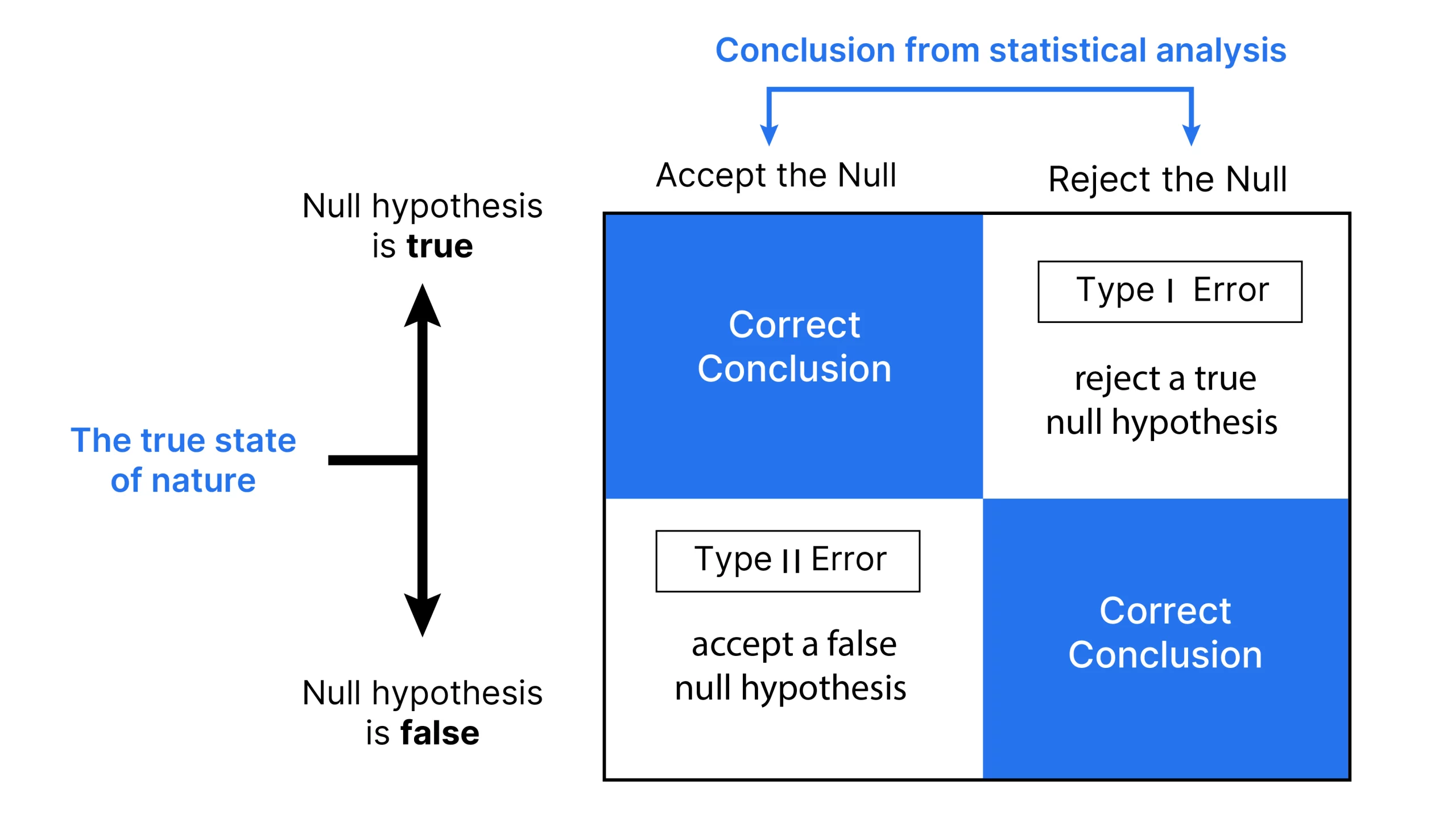
While these scenarios underscore the importance of grasping the nuances of Kind I and Kind II errors in statistical analysis? False positives, also known as kind I errors, occur when a true null hypothesis is incorrectly rejected. Type II errors, also known as false negatives, result from failing to reject a false null hypothesis. Many statistical concepts revolve around minimizing these errors, albeit eliminating them completely is statistically impossible. Through a deeper comprehension of these concepts, we will empower ourselves to make informed decisions across diverse domains, extending from the healthcare realm to the pursuit of excellence in industrial production processes.
Overview
- Kind I errors and Kind II errors categorize false positives and false negatives respectively, in the context of specification testing.
- Speculative testing involves the formulation of null and alternative hypotheses, the selection of a suitable significance level, calculation of test statistics, and decision-making based on critical values.
- Kindly, errors occur when a genuine null speculation is mistakenly rejected, leading to unnecessary and potentially harmful interventions.
- Kind II errors occur when a false null hypothesis is not rejected, resulting in missed diagnoses or results that are overlooked.
- Balancing Kind I and Kind II errors necessitates considering trade-offs between significance levels, pattern sizes, and check energies to effectively mitigate both types of errors.
The Fundamentals of Speculation Testing
The test is a statistical method employed to decide whether ample evidence exists to refute a null hypothesis (H0) and accept an alternative hypothesis (H1). The method includes:
-
- No impact or no distinction.
- A difference in kind or degree exists.
- The typical threshold values for rejecting the null hypothesis (H₀), commonly specified at 0.05, 0.01, or 0.10.
- A metric calculated from pattern recognition, serving as a reference point to compare with an underlying value or standard.
- If the test statistic surpasses its critical value, reject the null hypothesis (H0); otherwise, fail to reject H0.
Additionally learn:
Kind 1 Error( False Constructive)
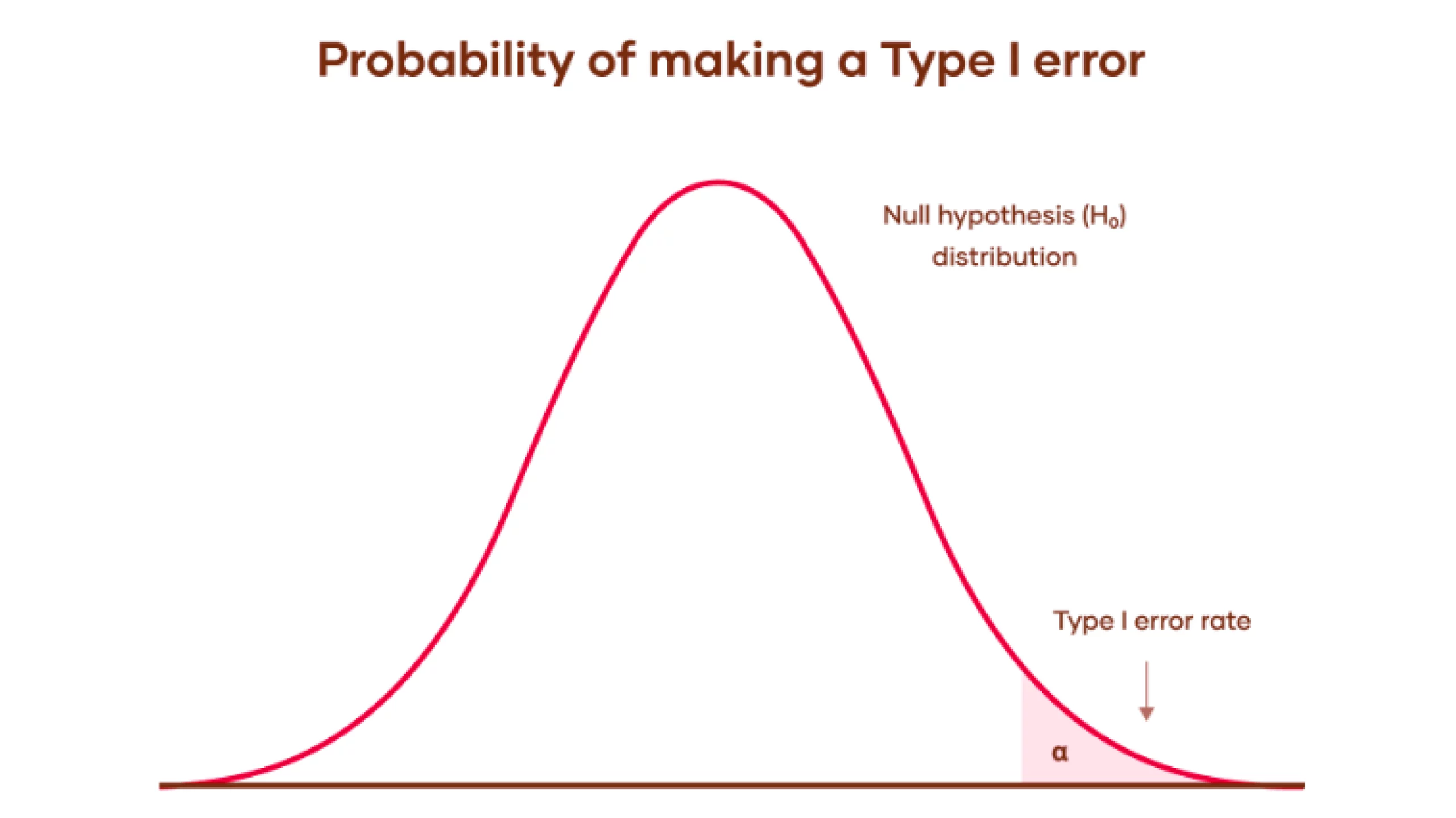
A Type I error occurs when a test’s null hypothesis (H0) is actually true but incorrectly rejected, often depicted in the graph below.
This anomaly represents identifying something as outdated, akin to a misinformed construct. A Type I error is typically characterized by a medical test that incorrectly detects a patient as having an illness when they are actually healthy, thereby triggering a false positive diagnosis. The null hypothesis (H0) would actually state: There is no significant difference in the prevalence of illness between the control group and the affected individual, suggesting that the affected person does not have a unique or distinctive illness.
The probability of committing a Type I error is commonly referred to as the significance level or alpha level. The concept is signified by the Greek symbol α (alpha), commonly referred to as the alpha phase. Rarely does an opportunity arise with a probability of 5% or 0.05. Typically, researchers are accustomed to accepting a 5% probability of mistakenly rejecting the null hypothesis when in fact it is true.
Inaccurate diagnoses can lead to futile treatments or interventions, causing unnecessary stress and potentially harming individuals.
- The bell curve illustrates the range of possible outcomes when the null hypothesis is assumed to be true. These outcomes seem to be a product of chance rather than any deliberate influence or differentiation.
- The shaded area beneath the tail of the curve represents the importance stage, denoted by alpha (α). The probability that a false positive result would occur by chance, assuming the null hypothesis is actually true? When one’s understanding of how language processes are executed is flawed, this often leads to a type of error known as a Kind I or false constructive.
There exists a kind of error which is false damaging.
A kind II error occurs when an unknown sound remains unheard. Failing to recognize a genuine threat means missing the opportunity to raise the alert when necessary. In this context, the null hypothesis (H0) still posits that “no bear is present.” If an investigator fails to detect a bear despite its actual presence, they commit a Type II error.
The crucial aspect is not whether an illness actually exists, but rather whether it can be accurately diagnosed and identified. The potential for misdiagnosis lies in two scenarios: overlooking an existing condition or mistakenly diagnosing a non-existent one.
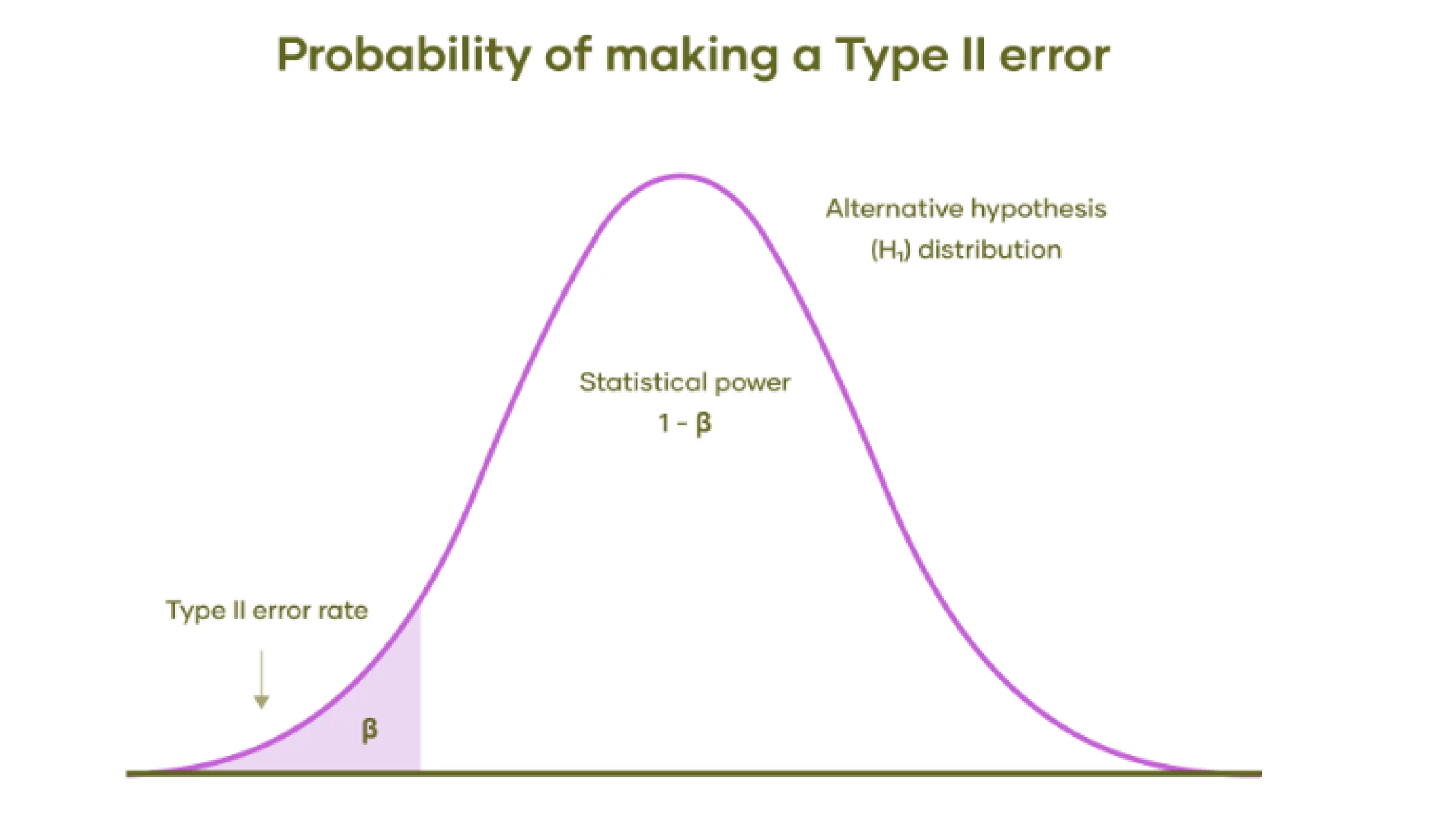
The probability of committing a Type II error, typically represented by the Greek symbol β (beta), measures the risk of failing to reject a false null hypothesis. The worth of this concept lies in its ability to quantify a check’s statistical energy, which is precisely calculated as one minus the product of (one minus beta) and beta.
Kindle II errors can have far-reaching consequences, potentially leading to the misdiagnosis of conditions and the failure to detect important test results, ultimately resulting in inadequate treatment or intervention.
- The bell curve illustrates the range of potential outcomes that would occur if a prediction or hypothesis holds true? There exists a discernible difference or consequence, in contrast to the notion of nothingness.
- The shaded region beneath the left tail of the distribution illustrates the probability of a Type II error.
- The unshaded area beneath the curve roughly equals the total statistical energy contained within the shaded region. Power? Increasing energy levels leads to a reduction in the likelihood of committing a Type II error.
Additionally learn:
The notion that Kind I and Kind II errors are comparable in nature remains a topic of ongoing debate.
Here is the improved text in a different style:
Detailed Comparisons:
| Side | Kind I Error | Kind II Error |
|---|---|---|
| The notion that we should accept unfounded claims as factual is a fallacy waiting to undermine the credibility of our entire endeavour. | The notion of accepting a false null hypothesis. | |
| α (alpha) | β (beta) | |
| Equivalent in magnitude to the standard established for verification. | Calculated as (1 – energy), reflecting the inverse relationship between energy and the measure. | |
| What’s the original text you’d like me to revise in a different style? | What a fascinating concept? | |
| Likelihood or luck | Lower pattern sizes or significantly fewer robust statistical tests | |
| The occurrence of an “unintended alarm” within a detection protocol. | “Miss” in a detection system | |
| Incorrectly rejecting the null speculation | The tendency to accept as true a claim that has no basis in fact is a common pitfall. | |
| Consequences arise when tolerance levels are set too broadly. | When acceptance standards are overly stringent, opportunities may slip away. | |
| In high-stakes domains where accuracy is paramount (e.g., medical diagnostics), minimizing false positives assumes paramount importance. | In high-stakes environments where a single misdiagnosis can have devastating consequences, prioritizing accuracy in fields such as medical screenings that detect life-threatening conditions is crucial. |
Additionally learn:
The subtle nuances between Type I and Type II errors in statistical analysis warrant a closer examination.
There exists a fundamental trade-off between Type I and Type II errors. As reducing the likelihood of one type of mistake often inadvertently amplifies the risk of another.
- While decreasing α minimizes the likelihood of a Type I error, it simultaneously amplifies the risk of a Type II error. Rising alpha levels have a significant, albeit underappreciated, impact on various aspects of life.
- Raising the pattern measurement can effectively mitigate both Type I and Type II errors by providing more accurate estimates through larger sample sizes.
- Boosting the test’s efficacy by increasing the pattern size or employing more refined tests can significantly decrease the risk of Type II errors.
Conclusion
Kindly, types I and II errors are fundamental concepts in statistical theory and analytical methodologies. By grasping the nuances between these errors and their far-reaching consequences, we can elevate our interpretation of analytical results, perform more insightful analyses, and make more informed decisions across various disciplines. While acknowledging that imperfections are unavoidable, the goal should be to address them effectively by considering the specific situation and possible consequences.
Regularly Requested Questions
Ans. Eliminating various types of errors proves challenging due to the fact that reducing one often results in an increase of another. Despite these efforts, however, inconsistencies may still arise from variations in the pattern measurement and meticulous design of the study.
Ans. Frequently perpetuated myths surrounding Type I and Type II errors persist, despite efforts to clarify their distinctions.
As α decreases constantly, it leads to an increasingly rigorous examination process.
While decreasing alpha may reduce Type I errors, it could potentially exacerbate Type II errors, leading to the omission of genuine positive findings.
Large-scale patterns render obsolete concerns over such mistakes.
Actually, large pattern sizes can reduce errors but do not eliminate them entirely. The cornerstone of effective inquiry remains a well-crafted research design.
A major consequence (p-value < α) means the null speculation is fake.
Although a significant result opposes the null hypothesis H₀, it does not necessarily imply that H₀ is false. Various components such as research design and context must be taken into consideration.
Ans. Raising the sensitivity of your checks makes it even more likely to detect genuine impacts. By leveraging your unique strengths and interests.
A. Rising your pattern measurement.
B. Utilizing extra exact measurements.
C. Lowering variability in your knowledge.
D. Elevating the effectiveness of impact measurement, where feasible.
Ans. Pilot research enables the estimation of parameters necessary for designing a larger, more definitive study. Their provision of preliminary insights into impact size and variability serves to underpin your pattern measurement calculations, thereby promoting stability by mitigating both Type I and Type II errors within primary research.

