What’s an Eigenvector and Eigenvalue?

Linear algebra lies at the foundation of numerous advanced mathematical concepts and is widely applied in knowledge science, machine learning, computer vision, and engineering. In the realm of linear algebra, a fundamental concept is that of eigenvectors, often accompanied by their corresponding eigenvalues. What lies at the heart of linear transformations: eigenvectors, a fundamental concept that unravels the intricacies of matrix algebra.

This text clearly explains the concept of eigenvectors in an accessible and straightforward manner, making it possible for anyone to understand.

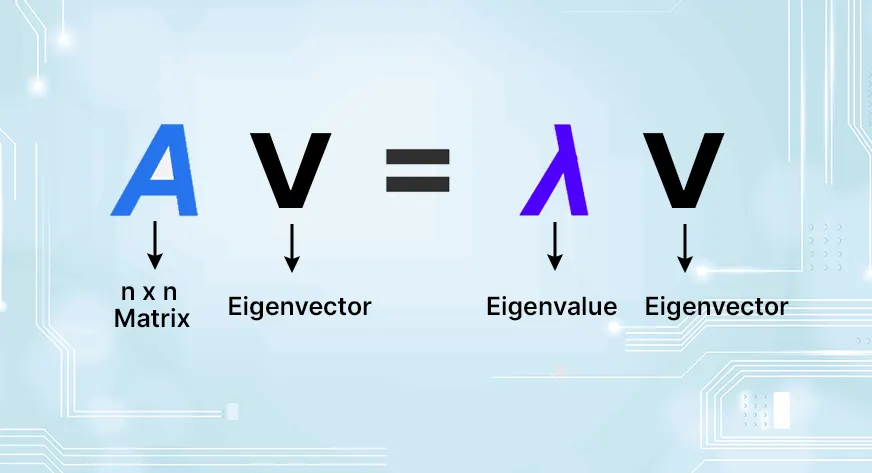
What’s an Eigenvector?

A sq. Matrix multiplication is often associated with a particular kind of vector referred to as an eigenvector. When the matrix operates on an eigenvector, it preserves the direction of the eigenvector intact, merely multiplying it by a scalar known as the eigenvalue.

For a square matrix, Matrix A and a non-zero vector v are such that:

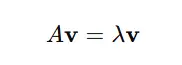
Right here:

• A is the matrix.
• v is the eigenvector.
• The eigenvalue λ is a scalar that represents the amount of change in the system after being transformed by the eigenvector.

Instinct Behind Eigenvectors

Consider a matrix A that embodies the properties of a linear transformation, capable of manipulating a 2D house through various means such as stretching, rotating, or scaling? When applying this transformation to a vector v:

• Many vectors undergo modifications in both their direction and scale.
• Certain specific vectors are merely scaled without being rotated or flipped. These particular vectors are eigenvectors.

For instance:

• If λ>1, the eigenvector is stretched.
• If 0<λ<1, the eigenvector is compressed.
• If λ = -1, the eigenvector reverses its direction but preserves its magnitude.

Why Are Eigenvectors Essential?

Eigenvectors perform a pivotal role in various mathematical and practical applications.

1. PCA is a widely utilized approach to reducing dimensionality effectively. Eigenvalues are employed to identify the primary components of data, capturing the maximum variability and enabling the determination of key factors.
2. The algorithm ranking internet pages leverages eigenvectors of a matrix illustrating hyperlink connections between online pages. The principal eigenvalue plays a crucial role in determining the relative importance of each webpage.
3. In physics, eigenvectors and eigenvalues define the fundamental states of a system and their quantifiable characteristics, directly relating to distinct vitality spectrums.
4. Eigenvectors play a crucial role in facial recognition systems, particularly in techniques such as Eigenfaces, where they enable images to be represented as linear combinations of principal components.
5. Eigenvectors play a crucial role in engineering by modeling the modes of vibration that occur in structures such as bridges and buildings.

Easy methods to Compute Eigenvectors?

To find eigenvectors, follow this procedure:

• (A – λI)v = 0 Remedy for eigenvalues: Discover eigenvectors:
• Determine the characteristic equation by computing det(A – λI) = 0 to find the eigenvalues λ.
• Determine the value of λ that satisfies the equation (A-λI)v = 0, then solve for v to obtain a non-trivial solution.

Instance: Eigenvectors in Motion

Take into account a matrix:

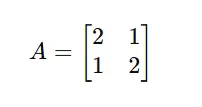
Step 1: Discover eigenvalues λ.

Remedy det⁡(A−λI)=0:

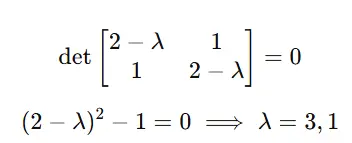
Discovering eigenvectors for each eigenvalue λ.

For λ=3:

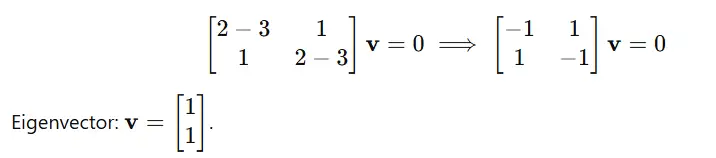
For λ=1:

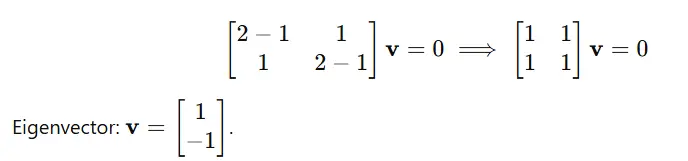
Python Implementation

What are the eigenvalues and eigenvectors of the matrix you want to analyze?

Instance Matrix

Take into account the matrix:

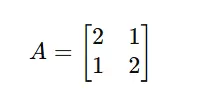
Code Implementation

import numpy as np np.set_printoptions(precision=4) A = np.array([[2, 1], [1, 2]]) eigenvalues, eigenvectors = np.linalg.eig(A) eigenvalues = eigenvalues.real eigenvectors = eigenvectors.real print("Matrix A:") print(A) print("\nEigenvalues:") print(eigenvalues.reshape(-1, 1)) print("\nEigenvectors:") print(np.round(eigenvectors, decimals=4)) 

Output:

Matrix A: [[2 1]  [1 2]] Eigenvalues: [3.  Eigenvectors: [0.707106781  -0.707106781;  0.707106781  0.707106781] 

Visualizing Eigenvectors

One can intuitively grasp how eigenvectors respond to the linear transformation defined by matrix A.

Visualization Code

import matplotlib.pyplot as plt eig_vec1 = eigenvectors[:, 0] eig_vec2 = eigenvectors[:, 1] plt.quiver(0, 0, eig_vec1[0], eig_vec1[1], angles='xy', scale_units='xy', scale=1, color='r', label='Eigenvector 1') plt.quiver(0, 0, eig_vec2[0], eig_vec2[1], angles='xy', scale_units='xy', scale=1, color='b', label='Eigenvector 2') plt.xlim(-1, 1) plt.ylim(-1, 1) plt.axhline(0, color='grey', linewidth=.5) plt.axvline(0, color='grey', linewidth=.5) plt.grid(color='lightgray', linestyle='--', linewidth=.5) plt.legend() plt.title('Eigenvectors of Matrix A') plt.show() 

This code generates a plot that visualizes the eigenvectors of A*A, showcasing their directions and stability under transformations.

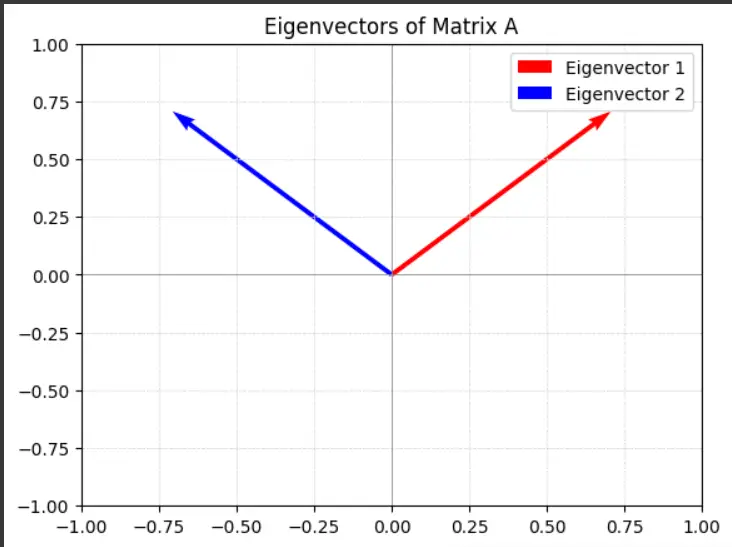
Key Takeaways

• Eigenvectors are specific vectors that remain unchanged in direction after being transformed by a matrix.
• Paired with eigenvalues, they determine the extent to which eigenvectors are scaled.
• Eigenvalues play a pivotal role in several fields, including knowledge science, machine learning, engineering, and physics.
• Python provides tools such as NumPy to easily calculate eigenvalues and eigenvectors.

Conclusion

Eigenvectors serve as a foundational concept across numerous disciplines, including knowledge science, engineering, physics, and beyond. Matrix transformations are crucial in fields such as dimensionality reduction, image processing, and vibration analysis, as they elucidate the fundamental effects of these transformations on specific operations.

Unlocking the power of eigenvectors, a fundamental mathematical concept, enables the resolution of complex problems with unparalleled accuracy and clarity. Using Python’s robust libraries, such as NumPy and SciPy, the process of computing eigenvectors becomes straightforward, enabling you to effectively visualize and apply these concepts in real-world scenarios.

While mastering the intricacies of eigenvectors may seem daunting, it’s a fundamental skill that can greatly benefit mathematicians and scientists alike, regardless of whether they’re building theoretical frameworks or exploring experimental data.

Ceaselessly Requested Questions