Information to lightning-fast JAX

Hey there, fellow fanatic! Have you ever wished for your code to run at supersonic speed? Meet JAX!. A cutting-edge companion for your machine learning, deep learning, and numerical computing adventures? Meet NumPwr: The Empowered Library It effortlessly handles gradients, compiles code for rapid execution using Just-In-Time (JIT) compilation, and seamlessly runs on graphics processing units (GPU) and tensor processing units (TPU), without batting an eyelid? Whether building complex neural networks, processing large datasets, fine-tuning transformer models, or seeking to accelerate computational workflows, JAX provides robust support and streamlined functionality for a wide range of applications. What sets JAX apart?

This comprehensive overview provides a detailed insight into JAX and its extensive environment.

Studying Goals

• JAX’s core ideas revolve around differentiating through the entirety of your program’s execution pipeline, which empowers you to automatically generate gradients for any computation, not just specific layers within a neural network.
• JAX’s three key transformations: map, batch, and tile! import jax
  import jax.numpy as jnp

  # Replace numpy with jax.numpy
  jnp.array([1, 2, 3])
  jnp.mean(jnp.array([1, 2, 3]))
  jnp.sum(jnp.array([1, 2, 3]))
  jnp.dot(jnp.array([[1, 2], [3, 4]]), jnp.array([[5, 6], [7, 8]]))

• Eliminate and rectify pervasive performance impediments within JAX codebases to optimize overall system efficiency. To achieve accurate JIT (Just-In-Time) compilation while circumventing common pitfalls, consider the following best practices:

  Pitfall 1: Insufficient profiling data can lead to suboptimal performance. To mitigate this, ensure your profiler is well-configured and captures relevant information about your application’s runtime behavior.

  When compiling code dynamically, it is crucial to accurately predict how often specific methods will be invoked. To achieve this, leverage profiling data to identify the most frequently executed paths in your code.

  Pitfall 2: Failure to handle exceptions properly can result in unexpected crashes or slow performance. Implement robust exception handling mechanisms to prevent such issues.

  When compiling code dynamically, you must account for potential exceptions that may occur during execution. Implement try-catch blocks and error-handling mechanisms to ensure graceful recovery from errors.

  Pitfall 3: Over-optimization can lead to decreased performance due to increased compilation overhead. Strike a balance between optimization and compilation time by adjusting your profiling data and compiler settings.

  To achieve accurate JIT compilation, you must find the sweet spot where optimization is effective without incurring unnecessary compilation penalties.

  Pitfall 4: Ignoring type information during compilation can result in suboptimal performance or incorrect results. Leverage type information to inform your compilation decisions.

  When compiling code dynamically, it is essential to consider type information when making compilation decisions. This includes leveraging static analysis and runtime type information to generate optimized code that accurately reflects the underlying data types.

  Pitfall 5: Failure to handle multithreading can lead to unexpected behavior or performance issues. Implement proper synchronization mechanisms to ensure thread safety during JIT compilation.

  When compiling code dynamically in a multi-threaded environment, you must ensure thread safety and prevent concurrent access to shared resources. Implement locks, semaphores, or other synchronization primitives as necessary to maintain consistency and avoid race conditions.

  Pitfall 6: Ignoring compiler warnings can result in unexpected behavior or performance issues. Pay attention to compiler warnings and address them promptly.

  When compiling code dynamically, it is crucial to heed compiler warnings that indicate potential issues with your code. Addressing these warnings will help prevent runtime errors and ensure accurate JIT compilation.

  By avoiding these common pitfalls and implementing best practices for JIT compilation, you can achieve optimal performance while maintaining the reliability of your application.

• What are we optimizing? Automate pervasive machine learning computations leveraging JAX’s versatile paradigm.
• Optimize performance by leveraging JAX’s automated differentiation capabilities. Sustain eco-conscious computing with optimized matrix operations.
• Why debugging JAX-specific issues requires a combination of understanding JAX’s unique architecture and employing effective debugging techniques? Optimize algorithms to minimize memory usage in massive computational tasks.

What’s JAX?

JAX is a powerful framework for acceleration-oriented array computation and program transformation, specifically designed for high-performance numerical computations and large-scale machine learning applications. JAX is essentially NumPy amplified, seamlessly integrating familiar NumPy-style operations with automated differentiation capabilities and hardware-accelerated processing for enhanced performance. Combining the finest aspects from three distinct realms results in a truly exceptional experience.

• elegant syntax and array operation
• like computerized differentiation functionality
• A high-performance implementation of (Accelerated Linear Algebra) leveraging {hardware} acceleration and compilation benefits.

Why does JAX Stand Out?

What are the units that JAX sets aside in its transformations? These highly effective features can significantly modify your Python code:

• Simply-In-Time (SIT) compilation accelerates execution by optimizing code generation at runtime.
• Computerized differentiation enables efficient computation of gradients in machine learning models.
• What data scientists need to know about mechanically vectorizing for batch processing?

Here’s a fast look:

import jax.numpy as jnp
from jax import grad, jit

@jit
def square_sum(x):
    return jnp.sum(jnp.square(x))

gradient_fn = grad(square_sum)

x = jnp.array([1.0, 2.0, 3.0])
print(f"Gradient: {gradient_fn(x)}")

Gradient: [2. 4. 6.]

Getting Began with JAX

Here are the steps to get started with JAX: Underneath we’ll comply with a few easy steps to begin your JAX journey!

Step1: Set up

Organizing JAX is effortless for CPU-only utilization. Using JAX for extra information can add significant value to your work. By incorporating JavaScript API extensions, you can enhance the functionality of your project and make it more comprehensive.

Step2: Creating Atmosphere for Mission

Conquering the unknown? I’ve got just the setup for you!

To create a conda atmosphere on your mission, begin by installing Anaconda, the premier data science platform. Once installed, navigate to the terminal and type `conda create –name myenv python=3.9` to establish a new environment, ‘myenv’, with Python 3.9 as its interpreter.

Next, activate this new environment using `conda activate myenv`, followed by installing essential libraries for data manipulation, visualization, and machine learning: `conda install pandas numpy matplotlib scikit-learn`.

To ensure seamless integration with popular frameworks like TensorFlow or PyTorch, add the relevant packages: `conda install tensorflow` or `conda install pytorch`.

Finally, verify your environment’s integrity using `conda list`, ensuring all dependencies are in order.

Now you’re ready to tackle that mission!

Create a Conda environment for JAX:
conda create --name jaxdev python=3.11

Activate the environment:
conda activate jaxdev

Create a new directory titled "jax101":
mkdir jax101 && cd jax101

Step3: Putting in JAX

Fostering integration of JAX within the nascent atmospheric framework?

For CPU-only:
`pip install --upgrade pip && pip install --upgrade jax`

For GPU:
`pip install --upgrade pip && pip install --upgrade 'jax[cuda=12]'`

You’re now empowered to tackle real-world problems head-on. Let’s explore innovative concepts before diving into hands-on coding exercises. I will explain the ideas first, and then we’ll code together to gain a comprehensive understanding.

What’s holding you back from exploring a fresh library? I will outline the steps to respond to your query in a clear and straightforward manner, making sure they are easy to follow. 

Why Study JAX?

JAX is a key enabler of innovative workflows and scalable data pipelines, serving as a potent influence device in the realm of artificial intelligence. While NumPy is a reliable workhorse, JAX is a trendy power tool. While it demands an additional process and data, the benefits of increased productivity make it well worth the effort for complex computational tasks.

• Jax’s Just-In-Time (JIT) compilation enables its code to execute significantly faster than equivalent Pure Python or NumPy code, especially when running on GPU and TPUs.
• JAX isn’t limited to machine learning; its capabilities extend to scientific computing, optimization, and simulation with equal distinction.
• JAX fosters effective programming practices, yielding more readable and sustainably maintained code.

Here’s an improved version of the text in a different style: Transformations that imbue JAX with extraordinary capabilities are fundamental to harnessing its potential effectively, making a thorough comprehension of these underlying mechanisms essential for successful implementation.

Important JAX Transformations

What truly distinguishes JAX’s transformations is their departure from the typical numerical computation libraries like NumPy and SciPy. Let’s uncover the power of these libraries and see how they’ll revolutionize your coding experience.

JIT or Simply-In-Time Compilation

Just-in-time compilation optimizes code execution by compiling components of a program at runtime rather than ahead of time.

How JIT works in JAX?

In JAX, jax.jit Compiles a given Python operation into a just-in-time (JIT)-optimized model, enabling efficient execution. Adorning a operate with @jax.jit Captures its execution graph, optimizes it, and compiles the optimized graph using XLA. The compiled model then executes efficiently, yielding significant performance enhancements, especially in cases of repeated operation calls.

To successfully tackle this endeavor, one must first carefully consider the key elements involved.

@jit
def fast_function(x):
    for _ in range(1000):
        x = jnp.sin(x) + jnp.cos(x)
    return x

The two operations are essentially identical, with one being a straightforward Python compilation process and the other serving as JAX’s JIT (just-in-time) compilation process. The algorithm calculates the cumulative sum of 1,000 knowledge factors combining sine and cosine features. We will assess efficiency by evaluating time usage.

import jnp
x = jnp.arange(1000)

jnp.jit(fast_function)(x)  # First run compiles the function
start_time = time.time()
slow_result = slow_function(x)
print(f"Without JIT: {time.time() - start_time:.4f} seconds")

start_time = time.time()
fast_result = fast_function(x)
print(f"With JIT: {time.time() - start_time:.4f} seconds")

The outcome will undoubtedly leave you in awe. The just-in-time (JIT) compilation process proves to be a staggering 333 times faster than its traditional counterpart. Comparing apples to oranges, it’s akin to scrutinizing a Schwinn bike alongside a Bugatti Chiron.

Compared to original times: 0.0320 seconds

While Just-In-Time (JIT) compilation can significantly accelerate execution, its benefits are only realized when used judiciously; attempting to apply it elsewhere would be akin to driving a Bugatti on a rural road, offering little enhancement.

Widespread JIT Pitfalls

JIT excels when working with statically typed languages and data structures. Avoid using Python loops and conditional statements that rely on array values? JIT compilation does not support dynamic arrays in its current implementation.

# Dangerous - makes use of Python management circulation
@jit
def bad_function(x):
    if x[0] > 0:  # This would possibly not work nicely with JIT
        return x
    return -x


# print(bad_function(jnp.array([1, 2, 3])))


# Good - makes use of JAX management circulation
@jit
def good_function(x):
    return jnp.the place(x[0] > 0, x, -x)  # JAX-native situation


print(good_function(jnp.array([1, 2, 3])))

As the likelihood of bad_function being detrimental stems from the Just-In-Time (JIT) compiler failing to correctly position itself relative to the value of x during computation, there exists a pressing need for rectification.

[1 2 3]

Limitations and Issues

• The first time a JIT-compiled operation is executed, it incurs a one-time overhead due to the compilation process. While the compilation value may initially seem to overshadow the efficiency benefits, this distinction becomes less significant when considering smaller features or those solely focused on achieving a specific goal?
• to be public. Dynamic management of circulation, such as altering shapes or values through primary manipulation using Python loops, is not supported in the compiled code. JAX provides options such as `jax.lax.cond` and `jax.lax.scan` for managing dynamic control flow.

Computerized Differentiation

Computerized differentiation, or autodiff, is a computational method that enables precise and successful calculation of feature derivatives. The process plays a crucial role in refining machine learning models, especially during the training of neural networks, where gradient updates drive model parameter adjustments.

JAX’s computerized differentiation works by transforming a given function into an equivalent function that computes the derivative of the original function. This is achieved through the use of operators and techniques from automatic differentiation, such as reverse mode or forward mode. The resulting derivative function can then be used to compute gradients, Jacobians, or higher-order derivatives.

Autodiff operates by leveraging the chain rule of calculus to break down intricate functions into more straightforward components, then computes the derivatives of these sub-functions and ultimately aggregates the results. The process records each step taken during program execution to construct a computational graph, subsequently utilizing this graph to calculate derivatives effortlessly.

Auto differentiation’s two primary modes are computational and symbolic.

• Calculates derivatives efficiently via the computational graph, ideal for functions with a limited number of parameters.
• Calculates derivatives through a single pass of the computational graph, efficiently handling features with many parameters.

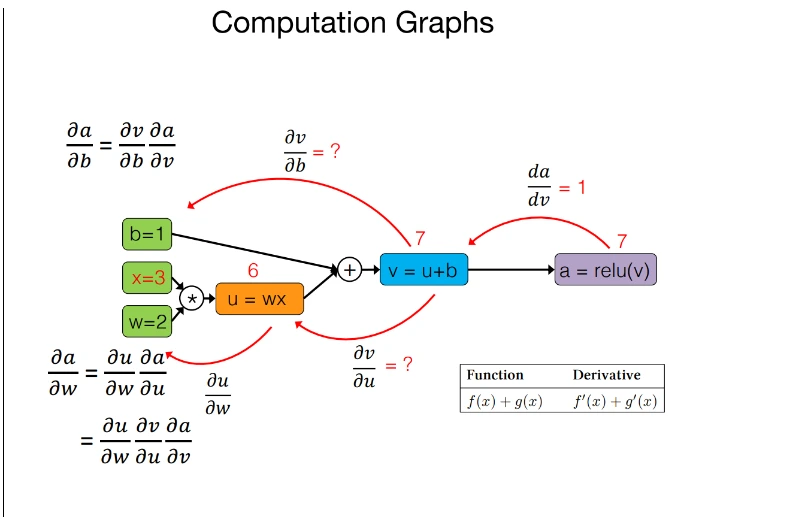
The core capabilities of JAX’s automatic differentiation (AD) mechanism include:

? finite differences, which approximate the derivative by evaluating the function at nearby points.

• JAX.grad calculates the derivative of a scalar-output function with respect to its input. When dealing with feature sets that accept multiple inputs, a partial derivative spin-off is feasible to obtain.
•   JAX enables efficient computation of high-order derivatives, mirroring complex Jacobian and Hessian matrices, thereby facilitating advanced optimization techniques and realistic physics simulations.
•   Autodifferentiation in JAX integrates effortlessly with various transformations such as `jax.jit` and `jax.vmap`, enabling efficient and scalable computation.
•   JAX’s auto-diff leverages reverse-mode differentiation for scalar-output features, rendering it highly efficient in deep learning applications.

import jax.numpy as jnp

def neural_network(params, inputs):
    weight, bias = params
    return jnp.dot(inputs, weight) + bias

def loss_fn(params, inputs):
    output = neural_network(params, inputs)
    return jnp.sum(output)

layer_grad = jax.grad(loss_fn, args=(0,))
value_and_grad = jax.value_and_grad(loss_fn, args=(0,))

key = jax.random.PRNGKey(0)
x = jax.random.normal(key, (1, 3, 4))
weight = jax.random.normal(key, (1, 4, 2))
bias = jax.random.normal(key, (1, 2,))

grads = layer_grad((weight, bias), x[0])
output, grads = value_and_grad(loss_fn, args=((weight, bias), x[0]))

twice_derivative = jax.grad(jnp.sin, 0)
print(f"Second derivative of sin at x=2: {twice_derivative(2.0)}")

The second derivative of sin(x) evaluated at x = 2 is sin(2)?

Effectiveness in JAX

• JAX’s computerized differentiation stands out as an environmentally friendly solution due to its seamless integration with XLA, enabling optimization at the machine code level, thereby minimizing computational overhead and energy consumption.
• The versatility of combining disparate transformations renders JAX a potent tool for building sophisticated machine learning pipelines and neural network architectures, including convolutional neural networks (CNNs), recurrent neural networks (RNNs), and transformer models.
• JAX’s syntax for automatic differentiation is remarkably straightforward and intuitive, allowing users to effortlessly compute gradients without requiring in-depth knowledge of XLA or complex library APIs.

JAX Vectorize Mapping

In JAX, the `vmap` operation is a powerful tool that automatically vectorizes computations, enabling you to apply a function to batches of data without manually writing loops. The function efficiently applies an operation to a specified array axis or multiple axes concurrently, potentially leading to significant performance boosts.

How vmap Works in JAX?

The vmap operation automates applying an operation to each element along a specified axis of an input array, while maintaining computational efficiency. This code transformation enables operations to efficiently process grouped inputs by leveraging vectorized computations.

By leveraging the power of parallel processing, vmap enables operations to be executed simultaneously across input axes through vectorization. By harnessing the capabilities of {hardware}, this approach enables the execution of SIMD instructions that process multiple data points simultaneously, thereby yielding significant performance enhancements.

Key Options of vmap

•   VAMP streamlines computation batching, effortlessly allowing developers to execute parallel code across batch dimensions without modifying the original operation’s logic.
•     Here’s a revised version of the text:

  The library integrates smoothly with various JAX transformations, mirroring the functionality of jax.grad for gradient calculations and jax.jit for just-in-time compilation, thereby enabling highly optimized and flexible code.

•   VMap enables seamless mapping across multiple input arrays or axes, rendering it an exceptionally adaptable tool for tackling various complex data processing and analysis scenarios involving multidimensional information or simultaneous manipulation of numerous variables.

import jax.numpy as jnp
from jax import vmap


def single_input_fn(x):
    return jnp.sin(x) + jnp.cos(x)


batch_fn = vmap(single_input_fn)

x = jnp.arange(1000)
result1 = jnp.array([single_input_fn(xi) for xi in x])
result2 = batch_fn(x)

print(result1.shape, result2.shape)

def two_input_fn(x, y):
    return x * jnp.sin(y)


vectorized_fn = vmap(two_input_fn, in_axes=(0, 0))
partially_vectorized_fn = vmap(two_input_fn, in_axes=(0, None))

print(result1.shape, result2.shape)
print(vectorized_fn(x, jnp.ones_like(x)).shape)
print(partially_vectorized_fn(x, jnp.ones_like(x)).shape)

(1000,)
(1000,)
(1000,3)

Effectiveness of vmap in JAX

• By utilizing vectorized computations, vmap significantly accelerates execution by harnessing the parallel processing capabilities of modern hardware, including GPUs and TPUs.
• This allows for more compact and legible code by eliminating the need for manual loops.
• VMap can be seamlessly combined with computerized differentiation (JAX.grad) to enable environmentally friendly computation of derivatives over batches of data.

When to Use Every Transformation

Utilizing @jit when:

• Operations are referred to multiple times using similar input formats.
• The system accommodates complex numerical calculations efficiently.

Use grad when:

• You want derivatives for optimization.
• Implementing machine studying algorithms
• Fixing differential equations for simulations

Use vmap when:

• Processing batches of knowledge with.
• Parallelizing computations
• Avoiding specific loops

The following linear algebra operations are utilized in this code snippet:

“`python
import jax
import jax.numpy as jnp
from jax.experimental import jax2tf

# Define the matrix A
A = jnp.array([[1, 2], [3, 4]])

# Define the vector x
x = jnp.array([5, 6])

# Matrix multiplication: A * x
result = jnp.dot(A, x)

# Transpose operation: A^T
At = jax2tf.jax_to_tf(jnp.transpose(A))

print(“Matrix Multiplication Result:”)
print(result)

print(“\nTranspose of the Matrix A:”)
print(At)
“`

JAX provides comprehensive support for matrix operations and linear algebra, making it well-suited for scientific computing, machine learning, and numerical optimization tasks. JAX’s linear algebra capabilities closely mirror those found in libraries such as NumPy, yet offer additional features including automated differentiation and Just-In-Time compilation to ensure optimized performance.

Matrix Addition and Subtraction

Operations are performed element-wise on matrices of identical structure.

import jax.numpy as jnp

A = jnp.array([[1, 2], [3, 4]])
B = jnp.array([[5, 6], [7, 8]])

# Matrix addition and subtraction
C = A + B
D = A - B

print(f"Matrix A:\n{A}")
print("===========================")
print(f"Matrix B:\n{B}")
print("===========================")
print(f"Matrix Addition of A+B: \n{C}")
print("===========================")
print(f"Matrix Subtraction of A-B: \n{D}")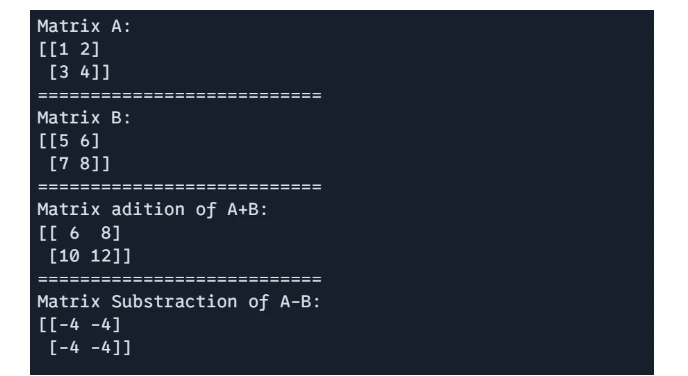

Matrix Multiplication

JAX helps with both element-wise multiplication (Hadamard product) and product-based matrix multiplication.

Matrix A: {{}}n{{}}
==============================
Matrix B: {{}}n{{}}
==============================n
Component-wise multiplication of A*B: [[{}]]n{}
==============================n
Matrix multiplication of A*B: {}n{}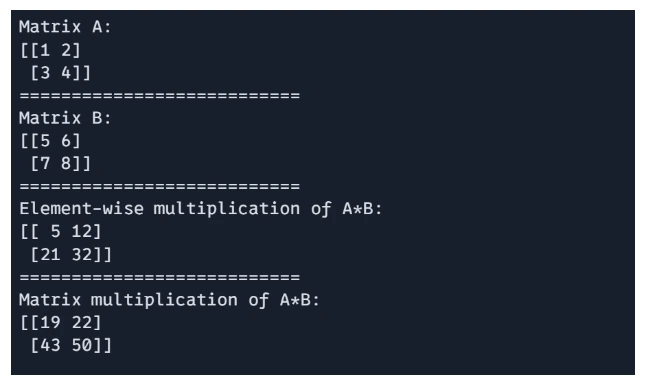

Matrix Transpose

The transpose of a matrix can be obtained using `jnp.transpose()`.

print(f"Matrix A:\n{A}\n===========================")
print(f"Matrix Transpose of A:\n{jnp.transpose(A)}")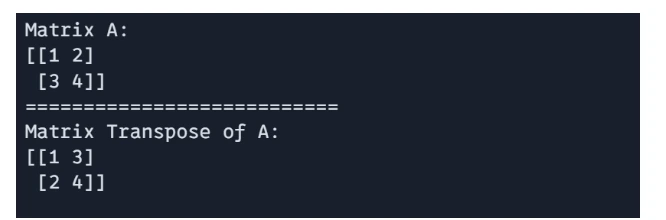

Matrix Inverse

JAX provides operations for matrix inversion using `jnp.linalg.inv()`.

print("Matrix A:")
jnp.set_printoptions(precision=3, suppress=True)
print(jnp.array_str(A))
print("===========================")
H = jnp.linalg.inv(A)
print("Matrix Inversion of A:")
jnp.set_printoptions(suppress=True)
print(jnp.array_str(H))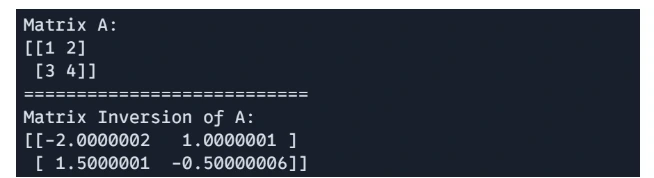

Matrix Determinant

The determinant of a matrix can be calculated using jnp.linalg.det().

print("Matrix A:\n", A)
print("================================")
print(f"Matrix Determinant of A: {jnp.linalg.det(A)}")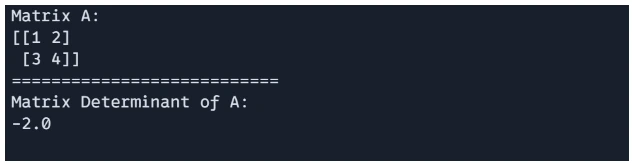

Matrix Eigenvalues and Eigenvectors

You can compute the eigenvalues and eigenvectors of a matrix using `jnp.linalg.eigh()`.

Matrix A:\n[[1, 2], [3, 4]]\n===========================\nEigenvalues of A:\n[0.37228132, -2.3722813]\n===========================\nEigenvectors of A:\n[[0.92387954, 0.38268343], [-0.38268343, 0.92387954]]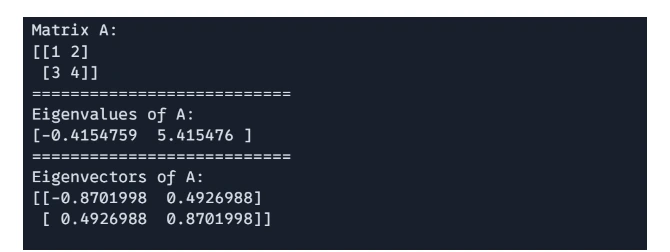

Matrix Singular Worth Decomposition

Singular Value Decomposition (SVD) is supported through the `jnp.linalg.svd` function, facilitating applications such as dimensionality reduction and matrix factorization.

# Singular Worth Decomposition(SVD)

import jax.numpy as jnp

A = jnp.array([[1, 2], [3, 4]])
U, S, V = jnp.linalg.svd(A)

print(f"Matrix A: n{A}")
print("===========================")
print(f"Matrix U: n{U}")
print("===========================")
print(f"Matrix S: n{S}")
print("===========================")
print(f"Matrix V: n{V}")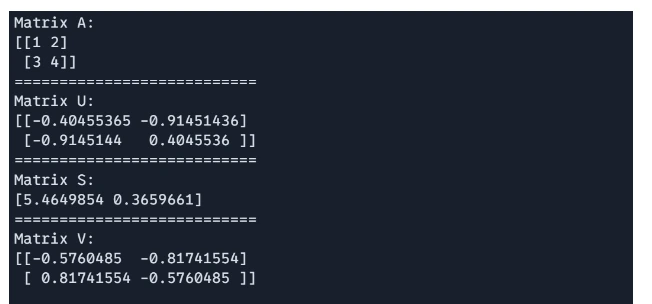

Fixing System of Linear Equations

To resolve a system of linear equations Ax = b, we employ jax.numpy.linalg.solve(), where A represents a square matrix and x is the solution vector. Matrix A must have the same number of rows as matrix B.

x = jnp.linalg.solve(A, b)

Worth of x: [1.8 1.4]

What are the ways to compute the gradient of a matrix operation?

By leveraging JAX’s computerized differentiation capabilities, one can efficiently calculate the gradient of a scalar function with respect to a matrix.
We will calculate the gradient of the underlying operation and values of X.

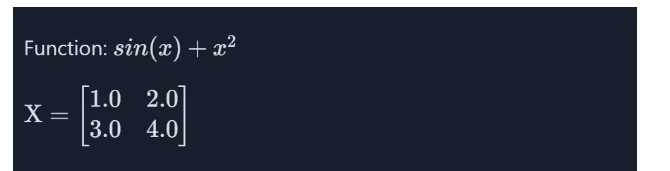
# Computing the Gradient of a Matrix Operate
import jax
import jax.numpy as jnp


def matrix_function(x):
    return jnp.sum(jnp.sin(x) + x**2, axis=1)


grad_f = jax.grad(matrix_function)
X = jnp.array([[1.0, 2.0], [3.0, 4.0]])
gradient = grad_f(X)

print(f"Matrix X: {X}")
print("===========================")
print(f"Gradient of matrix_function: {gradient}")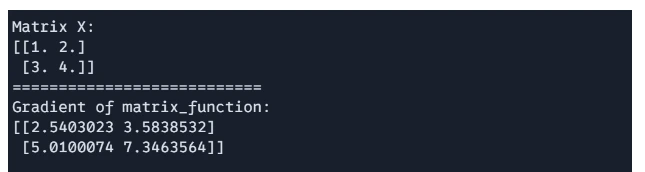

These operations are particularly useful for implementing JAX in numerical computing, machine learning, and physics calculations. Many hidden treasures await your discovery.

Scientific Computing with JAX

JAX’s highly effective libraries for scientific computing offer unparalleled performance capabilities, solidifying its position as the premier choice for this field due to its cutting-edge features such as just-in-time compilation, automated differentiation, vectorization, parallelization, and GPU-TPU acceleration capabilities. JAX’s potential to enhance computational efficiency makes it an ideal choice for a wide range of scientific applications, including physics simulations, machine learning, optimization, and numerical analysis.

We’ll uncover an optimization limitation in this area.

Optimization Issues

Let us navigate the optimisation challenges together.

The process to mitigate this issue will involve several key steps:

Identify the root cause of the problem
Analyze the current system and processes in place
Develop a plan to rectify the situation
Implement changes to prevent future occurrences

def rosenbrock(x):
    return sum((100*(y-x**2))**2 + (1-x)**2 for y,x in zip(x[1:],x[:-1]))

The Rosenbrock function, a fundamental benchmark problem in optimization, is detailed here. The function operates on an input array x, calculating a value that signifies its distance from the operation’s ideal minimum. The `@jit` decorator enables Just-In-Time (JIT) compilation, significantly accelerating computations by executing functions efficiently on both CPU and GPU architectures.

Step2: Gradient Descent Step Implementation

def optimize_rosenbrock(x0, learning_rate):
    @jit
    def rosenbrock(x):
        a = 5.0
        b = 100.0
        return a*(x[1]-x[0]**2) + (b-x[0])**2
    
    @jit
    def grad_rosenbrock(x):
        a = 5.0
        b = 100.0
        dx0 = 2*a*x[0]*(x[0]**2 - x[1]) + 2*(b-x[0])
        dx1 = 2*a*(x[1] - x[0]**2)
        return np.array([dx0, dx1])
    
    x = x0
    for _ in range(10000):
        x -= learning_rate * grad_rosenbrock(x)
    return x

This function executes a solitary iteration of the gradient descent algorithm for optimization purposes. The gradient of the Rosenbrock operator is computed using grad(rosenbrock)(x), providing the derivative with respect to x. The value of x is updated by subtracting the product of the gradient and a learning rate, effectively applying the gradient update using just-in-time compilation provided by the `@jit` decorator.

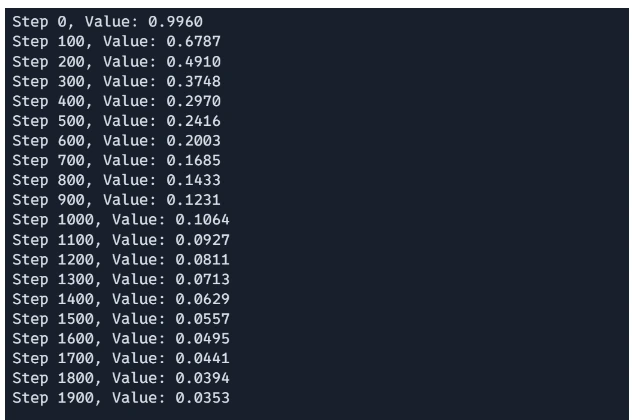
Step3: Working the Optimization Loop

x = jnp.array([0.0, 0.0])

learning_rate = 0.001

for _ in range(2000):

    x = gradient_descent_step(x, learning_rate)

    if i % 100 == 0:

        print(f"Step {i}, Worth: {rosenbrock(x):.4f}")

The optimization loop commences by initializing the starting point, x, and subsequently undertakes a thorough 1000-iteration execution of gradient descent. The gradient descent step operates primarily based on the current gradient in each iteration. As the Rosenbrock function is optimized every 100 steps, the current step quantity and its value at point x are displayed, providing a visual representation of the optimization’s progress.

The challenges of reconciling theoretical models with real-world complexities in physics. Can we leverage JAX to bridge this gap?

We’ll simulate the behavior of a bodily system by modeling the movement of a damped harmonic oscillator, an analogy that captures phenomena similar to those encountered in systems such as mass-spring mechanisms with friction, automotive shock absorbers, and oscillations in electrical circuits. Is it not good? Let’s do it.

Step1: Parameters Definition

import jax
import jax.numpy as jnp

mass_ = 1.0  # Mass of the thing in kilograms
damping_coefficient = 0.1  # Damping coefficient in kg per second
spring_fixed = 1.0  # Spring constant in Newtons per meter

time_step, whole_time = 0.01, 3000  # Time step and total time in seconds

Mass, damping coefficient, and spring constant are defined. The physical parameters governing the behavior of a damped harmonic oscillator are determined by these factors.

Step2: ODE Definition

def damped_harmonic_oscillator(state, t):
    """Compute the derivatives for a damped harmonic oscillator.

    Args:
        state (array): [x, v]
        t: time (not used in this autonomous system)
    Returns:
        array: [dxdt, dvdt]
    """
    x, v = state
    dxdt = v
    dvdt = -damping/mass * v - spring_constant/mass * x
    return jnp.array([dxdt, dvdt])

  The damped harmonic oscillator’s dynamics are defined by the time derivatives of position and velocity, effectively encapsulating a fundamental physical system.

Step3: Euler’s Methodology

def euler_step(state, t, dt):
    # Perform a single step of Euler's method for numerical integration
    derivative = damped_harmonic_oscillator(state, t)
    return state + dt * derivative

One straightforward numerical approach employed to solve the Ordinary Differential Equation (ODE). The algorithm predicts the system’s state at the next time step by extrapolating from its current state, incorporating spin-off effects.

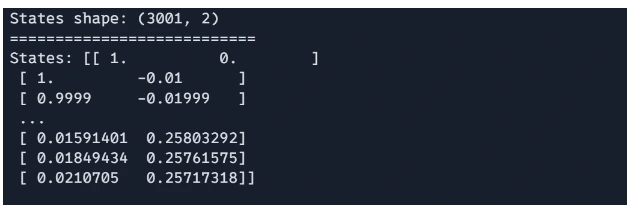
Step4: Time Evolution Loops

jnp.array([[1.0, 0.0]]), 
for _ in range(num_steps):
    states = jnp.append(states, [euler_step(states[-1], time, dt)])
    time += dt

The loop iterates a specified number of times, incrementally updating the system’s state using Euler’s method at each step.

Step5: Plotting The Outcomes

Finally, we will plot the outcomes to visualize the behavior of the damped harmonic oscillator.

import matplotlib.pyplot as plt

plt.style.use('ggplot')

positions = states[:, 0]
velocities = states[:, 1]
time_points = np.arange(0, (num_steps + 1) * dt, dt)

figsize=(12,6)
plt.figure(figsize=figsize)
plt.subplot(2, 1, 1)
plt.plot(time_points, positions, label='Position')
plt.xlabel('Time (s)')
plt.ylabel('Position (m)')
plt.legend()

plt.subplot(2, 1, 2)
plt.plot(time_points, velocities, label='Velocity', color='orange')
plt.xlabel('Time (s)')
plt.ylabel('Velocity (m/s)')
plt.legend()

plt.tight_layout()
plt.show()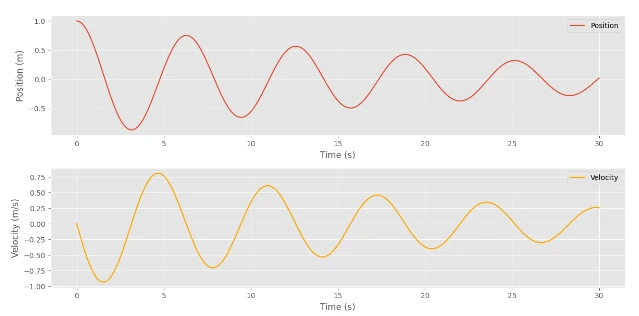

You want to explore building a Neural Community using JAX? Let’s explore the intricacies of this concept further.

As evident here, the values have steadily decreased over time.

Constructing Neural Networks with JAX

JAX is a powerful library that seamlessly blends high-performance numerical computing with the intuitive ease of NumPy-like syntax. This tutorial will guide you through the process of building a neural network using JAX, taking advantage of its unique features for automatic differentiation and just-in-time compilation to maximize performance.

Step1: Importing Libraries

Before building our neural network, we need to import the necessary libraries. JAX provides a suite of tools for conducting environmentally sustainable numerical calculations, while additional libraries facilitate the optimization and visualization of our results.

import jax
import jax.numpy as jnp
from jax import grad, jit, value_and_grad
from jax.random import.PRNGKey, regular
from optax import adam
import matplotlib.pyplot as plt

Step2: Creating the Mannequin Layers

Developing well-designed mannequin layers is crucial for establishing a robust architecture within our artificial neural network. Here is the rewritten text in a different style:

To kickstart efficient training, we will properly configure the dense layer parameters from the outset, thereby ensuring the model starts with pre-defined and informed weights and biases.

def init_layer_params(key, n_in, n_out):
    key_w, key_b = jax.random.split(key, 2)
    w = jax.nn.initializers.he_normal()(key_w, (n_in, n_out)) 
    b = jax.nn.initializers.zeros(())(key_b, (n_out,))
    return (w(), b())

def relu(x):
    return jnp.maximum(0, x)
    

• Initializing Operate:initiates layer parameters by setting weights (w) and biases (b) for dense layers using the He initialization method for weights, while assigning a small value to biases. While Kaiming He initialization excels for layers utilizing ReLU activation, other widely employed methods like Xavier initialization demonstrate improved performance for sigmoid-activated layers.
• Activation Operate: The ReLU operation applies the Rectified Linear Unit activation function to the inputs, setting all negative values to zero.

Step3: Defining the Ahead Move

The forward pass is the cornerstone of a neural network, as it determines how input data flows through the community to produce an output. Here, an approach is outlined to calculate the output of our model by applying transformations to the input data via initialized layers.

def ahead(params, x):
    """Ahead: Two-Layer Neural Network Activation"""
    weights_biases = params
    (w1, b1), (w2, b2) = weights_biases
    
    # First layer computation
    hidden_layer = relu(dot(x, w1) + b1)
    
    # Output layer computation
    output_logits = dot(hidden_layer, w2) + b2
    
    return output_logits
    

• Ahead Move: A head is implemented using a two-layer neural network, which calculates the output (logits) through a combination of linear transformations followed by ReLU activation, and additional linear transformations.

Step4: Defining the loss operate

A well-defined loss function is crucial for directing the training of our model.

As we proceed with the implementation, we’ll introduce the implied mean squared error (MSE) loss function, which quantifies the discrepancy between predicted and actual output values, thus guiding the model’s successful learning process effectively.

jnp.mean(jnp.square(pred - y))

• Loss Operate: The loss function computes the mean squared error (MSE) discrepancy between predicted logits and target class labels (y).

Step5: Mannequin Initialization

With our established mannequin architecture and loss function defined, we can now focus on initializing the model. This step involves setting the parameters for our neural network’s initial configuration, ensuring each layer commences training with randomized yet suitably scaled weights and biases.

def init_model(rng_key: jnp.ndarray, input_dim: int, hidden_dim: int, output_dim: int) -> jnp.ndarray:
    key1, key2 = jax.random.split(rng_key, 2)
    return [init_layer_params(key1, input_dim, hidden_dim), init_layer_params(key2, hidden_dim, output_dim)]
    

• Mannequin Initialization: The `init_model` function initializes the weights and biases for each layer of a neural network, providing a solid foundation for training and testing models. Two distinct random keys are employed to initialize the parameters for each layer separately.

Step6: Coaching Step

Training a neural network requires successive adjustments to its model parameters, driven by the calculated derivatives of the objective function.

This stage involves implementing a coaching operation that efficiently incorporates these updates, enabling our model to learn from the data across multiple epochs.

@jit
def train_step(params, opt_state, x_batch, y_batch):
    loss, grads = jax.grad(lambda p: loss_fn(p, x_batch, y_batch))(*params)
    _, opt_state = optimizer.update(grads, opt_state)
    params = optax.apply_updates(params, optimizer.get_updates())
    return params, opt_state, loss

• Coaching Step: The `train_step` operation executes a solitary iteration of gradient descent update.
• The function determines losses and gradients by employing the `value_and_grad` mechanism, a method that evaluates both values and differential gradients for a given operation.
• The optimiser updates are calculated, ensuring that mannequin parameters remain current and in sync.
• The is JIT-compiled for efficiency.

Step7: Information and Coaching Loop

To effectively train our mannequin, we must create relevant expertise and establish a continuous coaching cycle. This section will cover techniques for generating artificial knowledge for our instance and strategies for managing the training process across multiple batches and epochs.

def train_step(params, opt_state, x_batch, y_batch):
    with jax.enable_xla_jit():
        def loss_fn(params):
            return jnp.mean((jnp.dot(x_batch, params) - y_batch)**2)
        grad = jax.grad(loss_fn)(params)
        updates, opt_state = optimizer.update(grad, opt_state)
        params = optax.apply_updates(params, updates)
    return params, opt_state, loss_fn(params)

• Information EraRandomized coaching information (x_data) is generated alongside its corresponding objective (y_data) metrics. Initially, the mannequin’s parameters and the optimizer’s state are established.
• Coaching Loop: The neural networks undergo extensive training across multiple epochs, leveraging the efficiency of mini-batch gradient descent.       
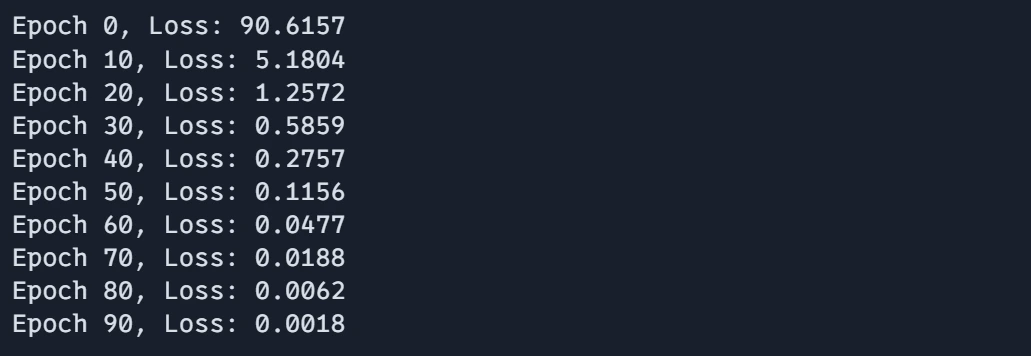
• The coaching loops iteratively traverse batches, executing gradient updates through the train_step operation. Typical losses are computed and recorded for each epoch. The epoch has completed with a total loss of.

Step8: Plotting the Outcomes

Envisioning the tangible results of coaching is crucial for gauging the effectiveness of our collective cognitive ecosystem. As we proceed with our project, we will now visualize the coaching loss across epochs to gauge the model’s learning progression and identify any anomalies or areas for improvement during the training process.

plt.figure(figsize=(8,6))
plt.plot(epoch_array, loss_array, label='Coaching Loss', marker='o')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Evolution of Coaching Loss over Epochs')
plt.grid(True)
plt.show()

Here are examples that demonstrate JAX’s remarkable ability to seamlessly merge exceptional efficiency with elegantly simple and readable code. The programming fashion inspired by JAX enables seamless composition of operations and effortless application of transformations, simplifying the development process.

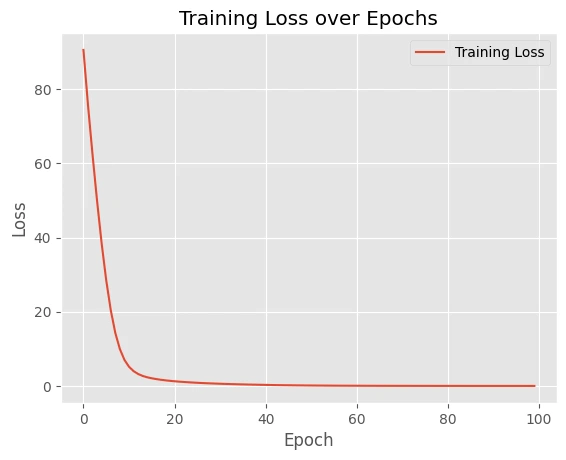
JAX’s unique strength lies in its ability to seamlessly integrate high-performance capabilities with elegant, easily comprehensible coding practices. The intuitive design of JAX-inspired programming enables seamless composition of operations and effortless application of transformations.

Finest Follow and Suggestions

When designing neural networks, following best practices significantly enhances their effectiveness and sustainability. This section delves into various strategies and recommendations for streamlining your code and amplifying the overall efficacy of your JAX-based models, thereby elevating their performance and versatility.

Efficiency Optimization

Optimising efficiency is crucial when utilising JAX, as it enables seamless harnessing of its full potential. Herein lies the opportunity to uncover innovative approaches for optimizing the performance of our JAX capabilities, thereby ensuring that our models execute expeditiously while preserving clarity.

JIT Compilation Finest Practices

Innovative Just-In-Time (JIT) compilation stands out as a key benefit of JAX, allowing for faster execution by dynamically compiling code at runtime. This section outlines best practices for effectively leveraging just-in-time (JIT) compilation, enabling you to sidestep common pitfalls and optimize the performance of your code.

Dangerous Operate

@jit
def improved_function(x, n):
    def inner(x):
        return lax.while_loop(lambda i, _ : jnp.less(i, n), lambda i, _: x + i, x)
    return inner(x)
    

The code iterates `n` times using a traditional Python for loop, incrementing the value of `x` by 1 with each pass. When using JIT compilation with JAX, the algorithm is optimized by unrolling the loop, potentially resulting in inefficiencies when dealing with large values of n. This strategy fails to fully harness JAX’s potential for optimization.

Good Operate

@njit
def improved_function(x, n):
    return x + n * np.ones(n) if isinstance(n, int) else x + n

This operation performs the same function, but utilizes a vectorized operation (x + n) instead of a loop, resulting in increased efficiency and reduced computational complexity. This approach yields significant environmental benefits due to JAX’s ability to optimise computations when expressed as a single, vectorised operation, thereby reducing computational complexity.

Finest Operate

# BETTER: Use scan for loops


@jit
def best_function(x, n):
    def body_fun(i, val):
        return val + 1

    return lax.fori_loop(0, n, body_fun, x)


print("===========================")
print(best_function(1, 1000))

Using JAX’s `jax.lax.fori_loop` effectively implements loops natively within the framework. The Lax.Fori_loop performs an identical increment operation as its predecessor, but achieves this using a compiled loop construct. The `body_fn` operation is defined to iterate over a range of values from `o` to `n`, leveraging the `lax.fori_loop` function to execute the operation in a loop. This approach outperforms traditional loop-unrolling methods in terms of environmental sustainability, making it a suitable solution for scenarios where the number of iterations remains uncertain until runtime.

:

===========================
===========================
1001
===========================
1001

The code showcases divergent strategies for handling loops and managing control flow within JAX’s JIT-compiled functions.

Reminiscence Administration

Effective environmental stewardship in computational frameworks is crucial, especially when dealing with massive data sets and complex models. This section will concentrate on prevalent pitfalls in reminiscence allocation and supply techniques for enhancing memory usage optimization in JAX.

Inefficient Reminiscence Administration

@jit
def efficient_function(x):
    energy_and_sin = jnp.stack((jnp.energy(x, 2), jnp.sin(jnp.energy(x, 2))), axis=-1)
    return jnp.sum(energy_and_sin, axis=-1)

The inefficient_function(x): A procedure that necessitates the creation of numerous temporary arrays – temp1 and temp2 – ultimately culminating in the calculation of their sum. As the frequency of array creation increases, so too does the risk of inefficient memory allocation and computational overhead, potentially leading to slower execution times and suboptimal resource utilization?

Environment friendly Reminiscence Administration

Combining operations efficiently is crucial in many applications. @jit def efficient_function(x): return jnp.sum(jnp.sin(jnp.energy(x, 2))) # Efficient single operation

This model condenses all operations into a concise, one-line expression. The function calculates the square of each part of the input value x, then applies the sine operation to each of these squared parts before summing up the results. By consolidating operations, it eliminates the need for temporary arrays, thereby reducing memory footprints and optimizing performance.

Check Code

x = jnp.array([1, 2, 3])
print(x)
print(inefficient_function(x))
print(efficient_function(x))

[1 2 3]
0.49678695
0.49678695

By harnessing JAX’s capabilities to optimize the computation graph, this environmentally friendly model significantly accelerates computations while conserving resources through reduced temporary array creation.

Debugging Methods

Debugging is a crucial component of the development process, especially in complex numerical computations where even minor errors can have significant consequences. Let’s accelerate the troubleshooting process for JAX with effective debugging techniques, allowing you to pinpoint and rectify issues swiftly.

JIT (Just-In-Time) compilation can significantly boost performance in Java applications. However, debugging such code can be a challenge due to its compiled nature at runtime. One way to tackle this is by utilizing print statements within the JIT compiler itself.

The code demonstrates effective techniques for troubleshooting within JAX, particularly when leveraging JIT-compiled capabilities.

import jax.numpy as jnp
from jax import debug


@jit
def debug_function(x):
    debug.print("Form of x: {}" , str(x))
    y = jnp.sum(x)
    debug.print("Sum: {}" , str(y))
    return y

# For advanced debugging purposes, disable Just-In-Time compilation
def debug_values(x):
    print(f"Enter: {x}")
    end_result = debug_function(x)
    print(f"Output: {end_result}")
    return end_result
    

• debug_function(x): This operates exhibit methods to effectively utilize debug.print() for in-depth debugging within JIT-compiled operations. In JAX, common Python print statements are not feasible within JIT due to compilation limitations, and therefore, the debug.print() function serves as a suitable alternative.
• The array x is printed in its original form using debug.print().
• After processing the cumulative total of the weather data for x, it displays the resultant sum using Debug.Print().
• The operate function finally returns the calculated sum y.
• The debug_values function enables a sophisticated debugging approach by temporarily exiting the Just-In-Time (JIT) compilation environment, allowing for more in-depth examination and analysis of program behavior. The program prints the input x using the built-in print function. The function subsequently invokes debug_function(x) to determine the ultimate outcome and ultimately prints the output before returning the results.

print("===========================")
print(debug_function(jnp.array([1, 2, 3])))
print("===========================")
print(debug_values(jnp.array([1, 2, 3])))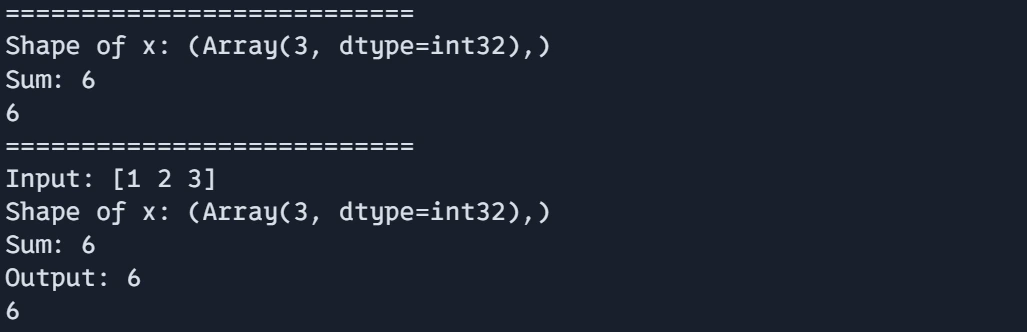

This approach enables the combination of in-JIT debugging via debug.print() with more comprehensive debugging outside the JIT using standard Python print statements.

JAX programming language has some widespread patterns and idioms that developers should know when writing efficient and readable code. For instance?

Ultimately, we’ll uncover broad patterns and idioms within JAX that can help streamline your coding process and boost efficiency. Mastering these practices will help you cultivate robust and efficient JAX functions.

Memory-Optimized Data Processing for Large-Scale Analytics

# 1. Machine Reminiscence Administration
def process_large_data(knowledge):
    chunk_size = 100
    outcomes = []

    for i in range(0, len(knowledge), chunk_size):
        chunk = knowledge[i:i + chunk_size]
        chunk_result = jit(process_chunk)(chunk)
        outcomes.append(chunk_result)

    return jnp.concatenate(outcomes)


def process_chunk(chunk):
    chunk_temp = jnp.sqrt(jnp.array(chunk))
    return chunk_temp

This operation processes massive datasets in manageable portions to prevent overburdening device memory.   

The code sets a chunk size to 100 and then processes each segment (or increment) of that fixed-length window independently, examining the data within those predetermined boundaries.   

By applying just-in-time (jit) compilation via process_chunk(), each chunk’s processing operation is optimized ahead of time, thereby enhancing overall performance and expediting execution.   

The results from each chunk are concatenated directly into a single array using `jnp.concatenate` (resulting in) to form a single record.

print("===========================")
knowledge = jnp.arange(10000)
print(knowledge.form)

print("===========================")
print(knowledge)

print("===========================")
print(process_large_data(knowledge))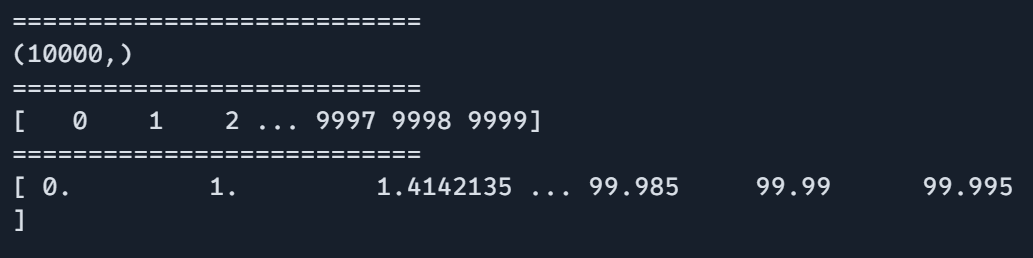

Reconciling the Imperatives of Reproducibility: A Guide to Harnessing Random Seeds in the Higher Information Age?

The operate create_traing_state() Ensures reliable management of arbitrary numerical generators (RNGs) in JAX, a crucial aspect for guaranteeing reproducible results and consistent outputs.

# 2. 

Defining and Utilizing Random Seeds

def create_training_state(rng):
    # Isolate distinct random number generators
    initial_rng, _ = jax.random.split(rng)
    params = init_network(initial_rng)

    return params, initial_rng  # Return new RNG for subsequent use
    

The process commences with a preliminary random number generator (RNG), which is subsequently divided into two distinct RNGs through the application of jax.random.split(). RNGs, responsible for distinct functions, initiate community parameters through `init_rng`, subsequently yielding updated RNGs for consecutive operations.

The operator returns both the initialised community parameters and the newly generated RNG for further utilisation, ensuring accurate handling of random states across various stages.

What are you referring to? Please provide the text you’d like me to improve in a different style as a professional editor.

===========================

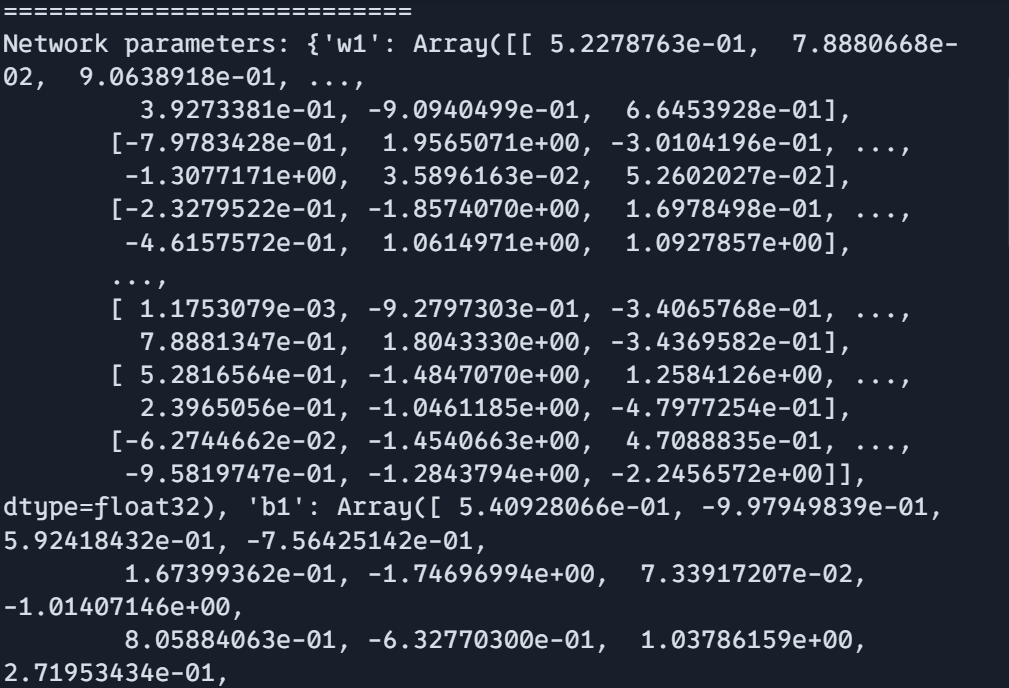
def init_network(rng):
    return {"w1": jax.random.normal(rng, (784, 256)), "b1": jax.random.normal(rng, (256,)), "w2": jax.random.normal(rng, (256, 10)), "b2": jax.random.normal(rng, (10,))}

key = jax.random.PRNGKey(0)
params, rng = create_training_state(key)

Random quantity generator: 0

dict_keys(['w1', 'b1', 'w2', 'b2'])

===========================

Community parameters form: (256,)

===========================

Community parameters form: ()

===========================

Community parameters form: (10,)

===========================

Community parameters: {'w1': DeviceArray([...], dtype=float32), 'b1': DeviceArray([...], dtype=float32), 'w2': DeviceArray([...], dtype=float32), 'b2': DeviceArray([...], dtype=float32)}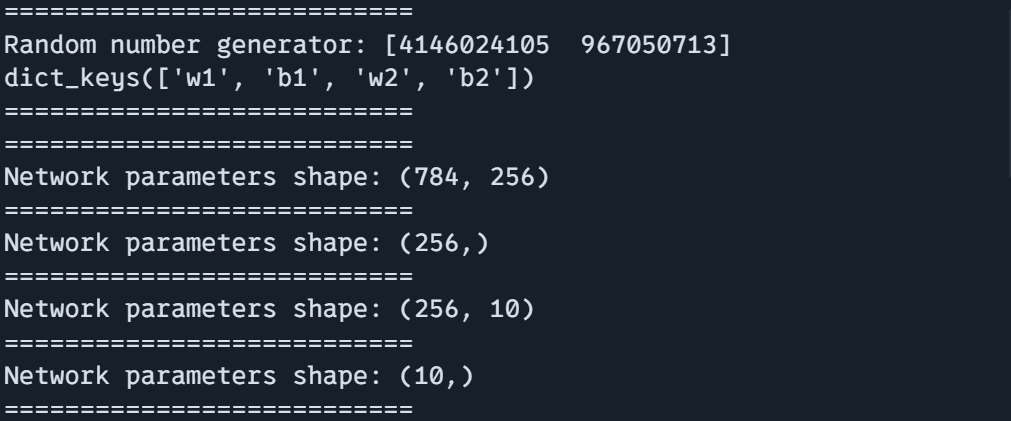

Utilizing Static Arguments in JIT

def g(x, n):
    i = 0
    whereas i < n:
        i += 1
    return x + i


g_jit_correct = jax.jit(g, static_argnames=["n"])
print(g_jit_correct(10, 20))

30

When compiling code just-in-time (JIT), a static argument is necessary if the operation involves the same arguments every time. Will this enhanced functionality streamline JAX feature utilization?   

from functools import partial


@partial(jax.jit, static_argnames=["n"])
def g_jit_decorated(x, n):
    i = 0
    whereas i < n:
        i += 1
    return x + i


print(g_jit_decorated(10, 20))

If you wish to use static arguments in just-in-time (JIT) compilation as a decorator, you must utilize `jit` within the `functools` module. partial() operate.

30

Now we’ve delved deeply into numerous captivating concepts and strategies in JAX and broader programming paradigms.

What’s Subsequent?

• Experiment with Examples: What’s the best way to master JAX transformations and APIs? Let’s embark on a mission!
• Discover Superior MattersParallel computing with pmap: Simplified scaling of computations using Google’s XLA compiler and parallelization capabilities.

All code used on this article is thoroughly tested for its functionality and efficacy before being published.

Conclusion

JAX (Jax.org) is a powerful tool that provides a range of capabilities for machine learning, deep learning, and scientific computing, enabling data scientists to accelerate their research and development efforts. Start by grasping the basics, experimenting liberally, and leverage the phenomenal documentation and community of JAX to gain support. While it’s true that there are many problems to learn and mastery won’t come from simply copying others’ code, genuine understanding only arises when one tackles the challenges independently? Let’s launch a localized project in Jacksonville immediately. The key takeaway is to preserve going, and learn how to do so effectively.

Key Takeaways

• With its NumPy-like interface and APIs, learning JAX becomes remarkably easy even for beginners. Most NumPy code requires minimal modifications to work seamlessly.
• JAX fosters straightforward, effective programming patterns, yielding well-organized, easily sustainable code and effortless evolution. Builders must ensure that Java Application eXtreme (JAX) is fully compatible with the principles of the Object-Oriented paradigm.
• JAX’s options excel due to the synergy of computerized differentiation and just-in-time compilation, rendering it remarkably well-suited for large-scale knowledge processing in an environmentally friendly manner?
• JAX (Jax.org) stands out for its exceptional capabilities in scientific computing, optimization, neural networks, simulation, and machine learning – making it a seamless choice for developers tackling various projects.

Steadily Requested Questions