While exploring the realm of TensorFlow Probability (TFP), we discovered straightforward ways to leverage these libraries for efficient sampling and robust density estimation.
To illustrate the fundamental principles of move development, we start with a distribution that exhibits a clear pattern, allowing for straightforward calculations of its density. We combine various invertible transformations to optimize data likelihood under a revised distribution that is ultimately remodeled through our optimization process. The efficacy of this log chance calculation lies in its ability to normalize flows effectively, yielding a log-likelihood under the unknown target distribution that can be expressed as the sum of the density under the base distribution of the inverse-transformed data, plus the absolute value of the log determinant of the inverse Jacobian.
Now, an affine transformation will rarely be sufficiently powerful to model complex, nonlinear phenomena. In stark contrast, autoregressive models have demonstrated substantial success in both density estimation and pattern recognition.
The concept of autoregressivity, bolstered by the confluence of cutting-edge architecture designs, characteristic engineering, and intense computational power, has driven the development of state-of-the-art models in domains such as image, speech, and video processing.
This submission will likely involve exploring the fundamental components of autoregressive flows within the TensorFlow Probability (TFP) framework. While we won’t be building cutting-edge models, we’ll explore fundamental concepts, empowering readers to perform their own experiments on their own data.
We’ll begin by examining autoregressivity and its implementation within TensorFlow Probability (TFP). We endeavour to approximate one of numerous experiments outlined in the “MAF paper”, serving as a proof-of-concept demonstration.
Finally, in our third installment on this blog, we revisit the task of analyzing audio data, with mixed results.
Autoregressivity and masking
In distribution estimation, autoregressive models emerge as a consequence of the chain rule of probability theory, which factors a joint density into a product of conditional densities.
Here: In autoregressive models, it’s necessary to establish an ordering among the variables, which may or may not be meaningful. Techniques employed include randomly assigning orderings and/or using distinct orderings for each layer.
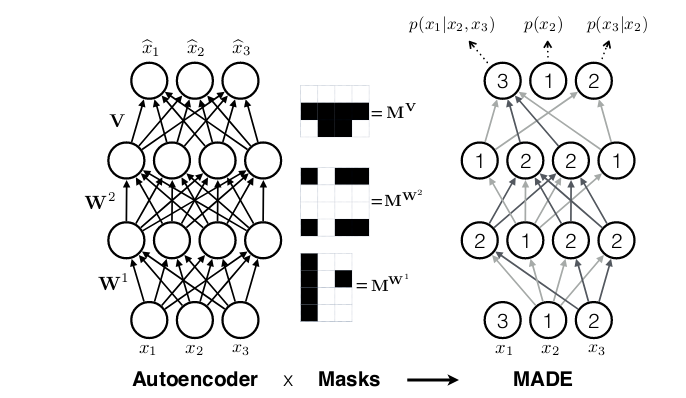
In recurrent neural networks, the conservation of autoregressivity arises naturally from the recurrence relation embedded in state updates, yet it remains unclear how this property can be preserved in a densely connected architecture.
In an environmentally conscious computing approach, a novel solution was presented, involving a dense connection layer that effectively blocks all unwanted connections – namely, those linking input features to the layer’s activation outputs. Activation may also be tied to entering options exclusively. When incorporating additional layers, meticulous attention must be paid to ensure that all necessary connections are effectively concealed, thereby guaranteeing that the final output will consistently and exclusively depend only on the original inputs.
Masked autoregressive flows combine the strengths of two distinct methodologies: autoregressive models, which don’t necessarily employ flow-based architectures, and flow-based models, which can operate independently of autoregressive components. In TFP, these opportunities are offered by. MaskedAutoregressiveFlowWhat is your design goal? Do you wish to create a new type of mathematical structure that combines the concepts of bijection and injection? A bijector could potentially offer enhanced flexibility and computational efficiency. However, its feasibility depends on various factors such as the specific application, problem domain, and existing mathematical frameworks. TransformedDistribution.
While the provided documentation offers straightforward guidance on utilizing this bijector, the gap between conceptual comprehension and implementing a “black box” may appear considerable. When faced with a situation reminiscent of the originator’s perspective, it can be tempting to delve deeper, scrutinizing whether assumptions accurately reflect reality. Let’s dive into the supply code with a sense of adventure.
By glancing ahead, we’ll construct a masked autoregressive model in TFP, leveraging the latest R bindings provided by TensorFlow.
Removing ambiguities, entities are pulled aside here. tfb_masked_autoregressive_flow The bijector is a function that maps inputs to unique outputs and vice versa, leveraging standard strategies. tfb_forward(), tfb_inverse(), tfb_forward_log_det_jacobian() and tfb_inverse_log_det_jacobian().
The default shift_and_log_scale_fn, tfb_masked_autoregressive_default_templateConstructs a self-contained neural community comprising hidden layers, each with a customizable number of nodes, activated by a user-defined function, and further tailored via adjustable parameters fed into the underlying mechanism? dense layers. The crucial requirement for these complex layers is to adhere to the autoregressive property. How does one achieve that sort of success? We’re sure able to accomplish this, as long as we’re not intimidated by some Python.
masked_autoregressive_default_template (now leaving out the tfb_ as we’ve entered Python land, leveraging masked_dense To implement what one might reasonably expect from an operation called this way: construct a densely connected layer that selectively excludes a portion of the loaded matrix. How? Let’s code then!
The rewritten text is:
The next set of code snippets are taken from masked_dense Here is the rewritten text in a different style:
In this context, we consider a basic 2×3 matrix layout.
(Note: I’ve kept the original sentence structure and wording as much as possible to maintain the same meaning while rephrasing it for better readability.)
The toy layer should consist of four distinct elements:
The masks are initially set to zero throughout. Why does contemplation seem destined to perform an element-wise multiplication on the load matrix, only to be perplexed by its unconventional structure? It’s natural to feel uncertain about the future, but trust that everything will unfold as it should.
array([[[0.], [0.], [0.]]], dtype=float32)To create a whitelist of authorized connections, we need to define specific instances where data transfer is permitted.
[[0. 0. 0.] [1. 0. 0.] [1. 1. 0.] [1. 1. 1.]]Yes? A transposition fixes form and logic simultaneously.
[[0.0, 1.0, 1.0, 1.0], [0.0, 0.0, 1.0, 1.0], [0.0, 0.0, 0.0, 1.0]]Now that we possess the masks, we’re poised to craft the layer – intriguingly, at present, it remains unclear whether tf.keras layer):
Masking occurs in two distinct approaches here. The initial loading process is obscured.
Additionally, a kernel constraint ensures that following optimization, all non-essential items are eliminated or set to zero.
Let’s add some excitement to our beloved playthings, shall we?
<tf.Tensor: id=30, form=(2, 4), dtype=float64, numpy= array([[ 0. [0.2491413, -0.14865185, 0.84920251] , -2.9958356 , -1.71647246, 1.09258015]])>Zeroes the place anticipated. After conducting a thorough examination of the load matrix,
<tf.Variable 'dense/kernel:0' form=(3, 4) dtype=float64, numpy= array([[ 0. [-0.748959, -0.4221494, -0.647345], , 0. [-0.00557496, -0.46692933], [ , -0. , -0. , 1.00276807]])>Good. Now, hopefully, after this little deep dive, issues have developed into even more concrete form. In larger models, the autoregressive property must be preserved across layers effectively.
While the concept of MAF holds significant promise in theory, its practical application remains largely untested on real-world datasets.
Masked Autoregressive Move
The MAF paper leveraged masked autoregressive flows, in combination with both single-layer and actual NVP, to a diverse range of datasets including MNIST, CIFAR-10, and others from this domain.
We select one of several publicly available datasets from the University of California, Irvine (UCI), a renowned repository for benchmarking machine learning models. Based on the results from the MAF authors, we will aim for the optimal configuration using 10 flow settings, which yielded the most effective outcomes in this dataset.
As accumulating data from the paper suggests,
- The information was derived solely from the file.
- discrete columns had been eradicated, in addition to all columns with correlations > .98; and
- The remaining eight columns had been standardized through z-transformation.
Regarding the neural community structure, we uncover its underlying patterns.
- Each of the ten MAF (Maximum Absolute Feature) layers was individually followed by a batch normalization operation.
- While considering the order of characteristics, the initial Most Able Feature (MAF) layer employed a variable ordering inherent in the provided dataset. Subsequently, each successive layer inverted this sequence.
- The use of sigmoid activation function, particularly for this dataset and in contrast to other diverse UCI datasets, served as a replacement.
- The Adam optimizer was employed, utilizing a learning rate of 0.0001.
- There have existed two latent layers for each Multivariate Autoregressive Forecasting (MAF), comprising precisely 100 items each.
- Coaching continued uninterrupted until a plateau was reached after 30 consecutive epochs without any discernible improvement on the validation set.
- The bottom layer’s distribution was modeled as a multivariate Gaussian.
However, that crucial piece of information is essential to accurately gauge this dataset, thereby rendering any attempts at estimation futile without it. Given knowledge of the dataset, it’s natural to wonder how authors would effectively manage its dimensional complexity: This is a time-series data set, where the MADE architecture previously introduced introduces auto-regressive relationships between options, rather than time steps. How can we effectively address the challenges posed by additional temporal self-referentiality in our modeling approach? The concept of a timeless universe remains an open issue in physics, with some theories suggesting that the passage of time may be relative rather than absolute. Within the authors’ phrases,
It’s a time series that was mistakenly treated as comprising independent and identically distributed (i.i.d.) instances. pattern from the marginal distribution.
While this dataset proves valuable for our present modeling endeavour, it also suggests that we must venture beyond MADE layers to accurately model time sequences.
Now, let’s examine an instance where MAF is applied to multivariate modeling, without considering temporal or spatial dimensions.
As per the guidelines provided by the authors, we take necessary actions.
Observations: 4,208,261 Variables: 19 $ X1 <dbl> 0.00, 0.01, 0.01, 0.03, 0.04, 0.05, 0.06, 0.07, 0.07, 0.09,... $ X2 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,... $ X3 <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,... $ X4 <dbl> -50.85, -49.40, -40.04, -47.14, -33.58, -48.59, -48.27, -47.14,... $ X5 <dbl> -1.95, -5.53, -16.09, -10.57, -20.79, -11.54, -9.11, -4.56,... $ X6 <dbl> -41.82, -42.78, -27.59, -32.28, -33.25, -36.16, -31.31, -16.57,... $ X7 <dbl> 1.30, 0.49, 0.00, 4.40, 6.03, 6.03, 5.37, 4.40, 23.98, 2.77,... $ X8 <dbl> -4.07, 3.58, -7.16, -11.22, 3.42, 0.33, -7.97, -2.28, -2.12,... $ X9 <dbl> -28.73, -34.55, -42.14, -37.94, -34.22, -29.05, -30.34, -24.35,... $ X10 <dbl> -13.49, -9.59, -12.52, -7.16, -14.46, -16.74, -8.62, -13.17,... $ X11 <dbl> -3.25, 5.37, -5.86, -1.14, 8.31, -1.14, 7.00, -6.34, -0.81,... $ X12 <dbl> 55139.95, 54395.77, 53960.02, 53047.71, 52700.28, 51910.52,... $ X13 <dbl> 50669.50, 50046.91, 49299.30, 48907.00, 48330.96, 47609.00,... $ X14 <dbl> 9626.26, 9433.20, 9324.40, 9170.64, 9073.64, 8982.88, 8860.51,... $ X15 <dbl> 9762.62, 9591.21, 9449.81, 9305.58, 9163.47, 9021.08, 8966.48,... $ X16 <dbl> 24544.02, 24137.13, 23628.90, 23101.66, 22689.54, 22159.12,... $ X17 <dbl> 21420.68, 20930.33, 20504.94, 20101.42, 19694.07, 19332.57,... $ X18 <dbl> 7650.61, 7498.79, 7369.67, 7285.13, 7156.74, 7067.61, 6976.13,... $ X19 <dbl> 6928.42, 6800.66, 6697.47, 6578.52, 6468.32, 6385.31, 6300.97,... # A tibble: 4,208,261 x 8 X4 X5 X8 X9 X13 X16 X17 X18 <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 -50.8 -1.95 -4.07 -28.7 50670. 24544. 21421. 7651. 2 -49.4 -5.53 3.58 -34.6 50047. 24137. 20930. 7499. 3 -40.0 -16.1 -7.16 -42.1 49299. 23629. 20505. The following data appears to be a numerical table with no contextual information provided. Therefore, it is unclear what the purpose of this data is or how it should be formatted. However, if I were to assume that this is some sort of scientific or statistical data, I might suggest reorganizing it into a more readable format, such as: |-47.1| |-10.6| |-11.2| |-37.9| As for the numerical values at the bottom, I would propose presenting them in a clearer format, possibly with labels or headers to provide context: | Data | Value | | --- | --- | | 48907 | | | 23102. | Please note that without further information about the purpose of this data, it is difficult to suggest more significant changes. 20101. 7285. 5 -33.6 -20.8 3.42 -34.2 48331. 22690. 19694. 7157. 6 -48.6 -11.5 0.33 -29.0 47609 22159. 19333. 7068. 7 -48.3 -9.11 -7.97 -30.3 47047. 21932. 19028. 6976. 8 -47.1 -4.56 -2.28 -24.4 46758. 21504. 18780. SKIPP 21125. 18439. SKIP 20836. 18209. With a staggering 4,208,251 additional entries?The Information Age Course of:
From 1800s to 1900s: The Industrial Revolution and Telegraphy.
To successfully assemble a movie, the crucial initial step required is establishing a solid bottom-line budget.
Now for the movie, by default, a construct built around batch normalization and the permutation of characteristic orders.
And configuring the optimizer:
How feasible are the possibilities beneath that isotropic Gaussian we chose as our base distribution?
The log-likelihood of this information beneath the remodelled distribution is remarkably low.
The values match – good. The coaching loop right here now could be a crucial moment. As we grow increasingly restless, we hasten the process by monitoring the log likelihood’s performance on the comprehensive test dataset, keenly gauging whether our efforts are yielding tangible improvements.
As our coaching and checkpoint systems processed over two million pieces of data each, we lacked the resources to replicate the exact same model as the authors. Despite any reservations, a single epoch’s output provides a straightforward conclusion: the setup seems to function reasonably well.
Epoch 1: Batch 1: -8.212026 --- check: -10.09264 Epoch 1: Batch 1001: 2.222953 --- check: 1.894102 Epoch 1: Batch 2001: 2.810996 --- check: 2.147804 Epoch 1: Batch 3001: 3.136733 --- check: 3.673271 Epoch 1: Batch 4001: 3.335549 --- check: 4.298822 Epoch 1: Batch 5001: 3.474280 --- check: 4.502975 Epoch 1: Batch 6001: 3.606634 --- check: 4.612468 Epoch 1: Batch 7001: 3.695355 --- check: 4.146113 Epoch 1: Batch 8001: 3.767195 --- check: 3.770533 Epoch 1: Batch 9001: 3.837641 --- check: 4.819314 Epoch 1: Batch 10001: 3.908756 --- check: 4.909763 Epoch 1: Batch 11001: 3.972645 --- check: 3.234356 Epoch 1: Batch 12001: 4.020613 --- check: 5.064850 Epoch 1: Batch 13001: 4.067531 --- check: 4.916662 Epoch 1: Batch 14001: 4.108388 --- check: 4.857317 Epoch 1: Batch 15001: 4.147848 --- check: 5.146242 Epoch 1: Batch 16001: 4.177426 --- check: 4.929565 Epoch 1: Batch 17001: 4.209732 --- check: 4.840716 Epoch 1: Batch 18001: 4.239204 --- check: 5.222693 Epoch 1: Batch 19001: 4.264639 --- check: 5.279918 Epoch 1: Batch 20001: 4.291542 --- check: 5.29119 Epoch 1: Batch 21001: 4.314462 --- check: 4.872157 Epoch 2: Batch 1: 5.212013 --- check: 4.969406 With these coaching outcomes, we consider the proof of concept to be largely successful. Despite our findings, it’s essential to note that the choice of hyperparameters also seems to play a significant role in determining the outcome. For instance, use of the relu activation operates as a substitute for tanh remained largely idle within the community that was focused on learning little to nothing. (As per the authors, relu successfully labored on diverse datasets that had undergone uniform Z-scaling.
Right here was compulsory – and this may apply to flows as well. Despite employing permutation bijectors, these models exhibited limited separability on this particular data set. The overall perception suggests that, when it comes to flows, we would both desire a “repository of strategies” – akin to the concept often referenced regarding GANs – or novel, innovative architectural designs (see “Prospects” below).
Lastly, we conclude with a familiar experiment revisiting our beloved audio data, previously showcased in two prior articles.
Analysing audio information with MAF
The dataset comprises 30 phrases, spoken through a diverse array of audio systems, each producing distinct variations in pronunciation. Earlier, a convolutional neural network (convnet) was trained to map spectrograms to the 30 distinct lessons. As a professional editor, I would improve the text in the following way:
To effectively substitute for one of many lessons, practice a Massive Open Online Course (MAF) on a single concept – say, the notion of “zero” – and engage the educated community to flag non-zero phrases as less plausible: proceed through the course in a systematic manner. A spoiler alert wasn’t necessary here, as there are no specific plot points or surprises being revealed. However, the text can still be improved for clarity and readability: The outcomes weren’t promising, and if you’re invested in this type of activity, consider a different approach (see “Outlook” below).
Despite our brevity, we swiftly summarize the achievements made, as this task exemplifies effective data processing where choices span multiple dimensions.
Pre-processing commences, adhering to the guidelines outlined in preceding discussions. While explicitly using keen execution is crucial, we must always hard-code identified values to ensure code snippets remain concise effectively.
Practicing the MAF on pronunciations of the phrase “zero” is a crucial step in enhancing our linguistic skills.
By implementing the methodology outlined in [reference], we aim to educate the community on utilizing spectrograms as a substitute for raw time-domain data.
Utilizing the identical settings for frame_length and frame_step
The QuickTime Fourier Transform model, as submitted, would yield data formatted A diverse array of frame types coupled with a multitude of Fast Fourier Transform coefficients.. What’s the original text you’d like me to improve? masked_dense() employed in tfb_masked_autoregressive_flow()As a result, we’re left with a substantial 25,186 combinations within the joint probability framework.
Within the established framework of the GAS instance, the lack of meaningful progress from the community is a direct outcome. The uncertainty was compounded by neither considering nor exploring the implications of leaving the information in a timely manner, with an astonishing 16,000 options within the joint distribution unexamined. Consequently, we elected to utilize the FFT coefficients calculated across the entire window, resulting in 257 collaborative possibilities.
Coaching was subsequently conducted in accordance with the established protocol used for the GAS dataset.
During coaching, we continuously tracked loglikelihoods across three distinct lessons: and. Log likelihoods for the initial ten epochs are presented below. The term “batch” pertains to the initial training cohort, whereas various other numerical designations denote full dataset collections, including both the comprehensive validation set and the three subsets selected for comparative analysis.
Epoch | Batch | Check | Cat | Hen | Wow -----|------|-------|----|-----|----- 1 | 1443.5 | 1455.2 | 1398.8 | 1434.2 | 1546.0 2 | 1935.0 | 2027.0 | 1941.2 | 1952.3 | 2008.1 | 3 | 2004.9 | 2073.1 | 2003.5 | 2000.2 | 2072.1 4 | 2063.5 | 2131.7 | 2056.0 | 2061.0 | 2116.4 | 5 | 2120.5 | 2172.6 | 2096.2 | 2085.6 | 2150.1 6 | 2151.3 | 2206.4 | 2127.5 | 2110.2 | 2180.6 | 7 | 2174.4 | 2224.8 | 2142.9 | 2163.2 | 2195.8 8 | 2203.2 | 2250.8 | 2172.0 | 2061.0 | 2221.8 | 9 | 2224.6 | 2270.2 | 2186.6 | 2193.7 | 2241.8 10 | 2236.4 | 2274.3 | 2191.4 | 2199.7 | 2243.8 While initial observations suggest no obvious risks, a comprehensive analysis reveals that 29 non-target lessons exhibit a stark disparity, with seven lessons outperforming the remaining 22, which exhibited a significant decline in log likelihood? We lack a mannequin for anomaly detection, which is a crucial component.
Outlook
While previous discussions have touched on this point, architectures that accommodate both temporal and spatial ordering may offer particularly valuable insights. The highly lucrative household is built upon sophisticated convolutional architectures, with recent advancements yielding further enhancements and innovations. Additionally, this mechanism can also mask and thereby render autoregressive, a characteristic that is inherent in both the hybrid model and the transformer-based architecture.
As we bring this submission to a close, it’s evident that the intersection of flows and autoregressivity played a crucial role, not to mention the innovative application of TFP bijectors. Future explorations may delve deeper into autoregressive models specifically, and who knows, perhaps even revisit audio data for a fourth time.

