Establish a Framework for Self-Supervised Learning: Step-by-Step Approach. While refining recurrent SSL models, we observe that the performance degradation follows a step-wise pattern on the left axis, while the learned feature representations progressively increase in complexity along the bottom axis. The direct visualisation of embeddings, substantiated by three fundamental PCA directives, reveals that initialisations collapse partially before expanding into a one-dimensional manifold, a two-dimensional manifold, and subsequently unfolding in tandem with iterative steps within the loss function.
Deep learning’s remarkable efficacy can largely be attributed to its ability to identify and distill meaningful abstractions from intricate data. Self-supervised learning (SSL) has emerged as a leading framework for extracting visual features directly from unlabeled images, analogous to how large language models (LLMs) learn linguistic representations from web-scraped text. Despite SSL’s prominent role in cutting-edge fashion trends, fundamental queries persist: What do self-supervised image programs ultimately study? How does this process unfold?
We present a novel approach to learning from our proposed simplified theoretical model, which we rigorously develop, by processing information through a series of distinct and well-defined stages. As we unveil this behavior’s far-reaching implications, it becomes evident that its consequences will resonate across a wide spectrum of cutting-edge applications currently in use.
This breakthrough unlocks fresh opportunities to refine SSL tactics, while prompting a wide range of innovative research queries that, once resolved, will offer a powerful framework for grasping the intricacies of cutting-edge deep learning applications.
Background
Here: We concentrate on joint-embedding SSL methods – a subset encompassing contrastive approaches – exploring representations that adhere to view-invariant criteria. The performance of these models features a critical component: learning matching embeddings for semantically equivalent “views” of an image. Notably, this uncomplicated approach produces remarkably accurate depictions in image-based tasks, even with minimal view variations such as random cropping and color manipulation.
Learning Principle: A Step-by-Step Approach to Studying in Secure Sockets Layer (SSL) with a Linearized Framework
Here is the rewritten text:
A precisely solvable linear model of SSL is initially described, enabling both training trajectories and closing embeddings to be expressed in a closed form. Notably, illustrations learning is compartmentalized into distinct stages; initially, the embedding ranking starts modestly, then incrementally increases in a step-by-step learning process.
Our research makes a significant theoretical contribution by accurately addressing the coaching dynamics of the loss function under gradient descent for specific instances, specifically linear models (f(x) = Wx). Here, we succinctly summarise our results, revealing that when initialization is minimal, the model acquires representations comprised solely of the top-d eigenvectors of the cross-correlation matrix (boldsymbol{Γ} ≡ E[xx^T]). We uncover that these principal directions unfold sequentially through distinct learning phases, punctuated by instances dictated by their attendant eigenvalues. The diagram illustrating this learning process demonstrates the growth of a novel pathway in the target function, accompanied by a corresponding decline in loss at each subsequent learning step. As an added benefit, we uncover a closed-form formula describing the ultimate embeddings achieved by the model upon convergence.
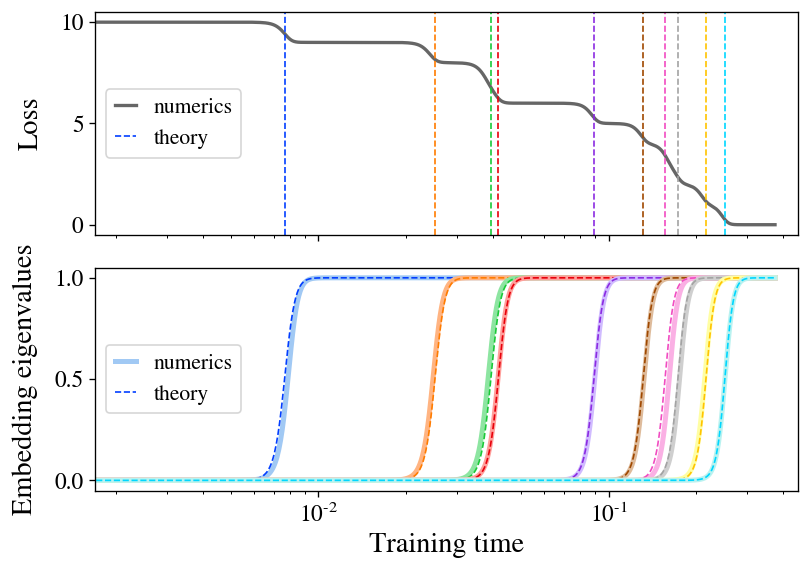
Determining Two: Stepwise Studying Appears to Follow a Non-Linear Model of Secure Sockets Layer (SSL). We train a linear model on a subset of CIFAR-10 data using the Barlow Twins loss function and verify its performance on a small pattern. The prime loss descends along a stair-step pattern, with each instance precisely forecasted by our theoretical framework. The eigenvalues of the embedded feature (located at the rear) emerge distinctly, precisely aligning with the corresponding conceptual representations (illustrated by dashed lines).
The discovery of stepwise studying exemplifies the fundamental concept of preferential learning, where many educational programs exhibiting roughly linear dynamics tend to focus on eigenvectors with larger eigenvalues. Recent research in traditional supervised learning has found that high-eigenvalue eigenmodes are learned more quickly during training. Our research uncovers equivalent findings for Secure Sockets Layer (SSL).
While the explanation for a linear manifold’s cautionary examination stems from the “neural tangent kernel” theory, it is crucial to note that studies have demonstrated that sufficiently large neural networks exhibit linear dynamics in their parameterization, a phenomenon confirmed by the research. The underlying truth enables a significant boost in resolution, enabling a straightforward extension from linear models to large neural networks – or, more broadly, arbitrary kernel machines – whereby the model selectively learns the highest-eigenvalue directions of an operator linked to the Neural Tangent Kernel. Examination of the NTK has revealed numerous insights into the coaching and generalization capabilities of even nonlinear neural networks, hinting that some of these findings might be translated into practical applications.
Experiments conducted using step-wise learning in SSL (Self-Supervised Learning) architectures, leveraging the power of Residual Networks (ResNets), demonstrated remarkable success in various computer vision applications.
As a key aspect of our research, we developed several primary SSL strategies using full-scale ResNet-50 encoders and observed that they are highly effective in recognizing stepwise learning patterns even in real-world scenarios, thereby underscoring the significance of this approach to the overall training process of SSL.
By visualizing the evolution of eigenvalues from the embedding covariance matrix as you implement ResNets in real-world scenarios, can we gain insight into stepwise studying? While applying the proposed approach can facilitate a gradual learning process by initializing parameters at a smaller scale, followed by a reduced training cost, this modification will be incorporated into the experiments discussed here and primarily focus on the standard case in our forthcoming paper.
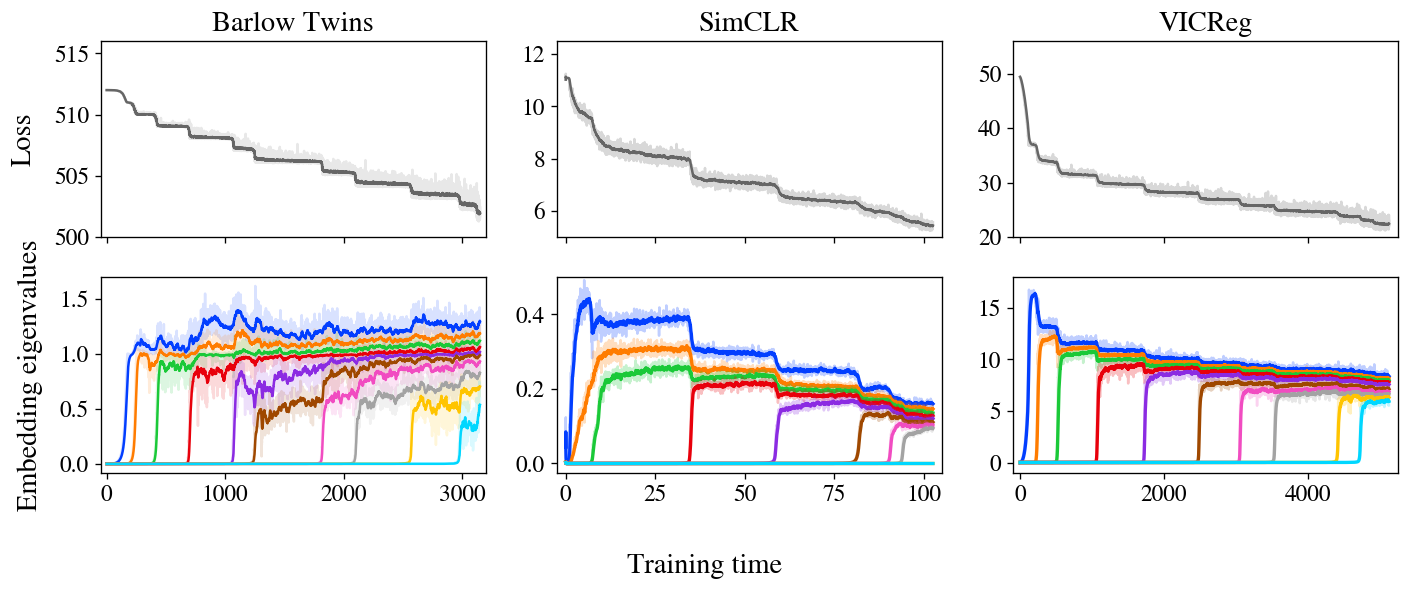
While determining similarities? The losses and embeddings of all three approaches exhibit a stepwise progression, with the embeddings incrementally improving in quality as expected by our model.
Three studies reveal losses and embedder covariance eigenvalues for three self-supervised learning (SSL) strategies – Barlow Twins, SimCLR, and VICReg – trained on the STL-10 dataset using standard augmentations. As remarkable losses materialize in a stair-step curve, each incremental step yielding an emergent eigenvalue, hitherto absent from the previous iteration. As seen in Figure 1, we provide a dynamic zoom-in animation illustrating the early developments of the Barlow Twins’ progression.
While initially appearing distinct, it’s long been speculated that these three approaches share a common thread despite their seemingly disparate nature. These various and distinct joint-embedding self-supervised learning strategies all achieve comparable efficacy on standard benchmark tasks. To identify the common thread running through these disparate approaches. While significant theoretical efforts have focused on identifying analytical parallels in the loss capabilities of various methods, our experimental findings suggest a distinct, overarching principle that unifies these approaches.
In a conclusive yet intriguing experiment, we investigate whether the actual embeddings produced by these methods align with theoretical predictions derived from the Neural Tangent Kernel (NTK) during training. While methodologies excel at bridging conceptual and experimental gaps within their frameworks, a more comprehensive examination reveals that diverse approaches share commonalities, further solidifying the notion that they are ultimately exploring similar ideas and can be harmonized.
Why it issues
By exploring the underlying theoretical framework of SSL methods, our research sheds light on how these approaches construct learned representations throughout training. What opportunities arise from this idea?
This image has potential to effectively support the application of SSL, both from an engineering perspective and by fostering a deeper understanding of SSL principles, ultimately enabling more comprehensive illustration studies.
While SSL methods are notoriously slow to train compared to their supervised learning counterparts, the underlying reason for this disparity remains unclear. Because our understanding of coaching implies that Secure Sockets Layer (SSL) coaching converges slowly, due to the later eigenmodes’ lengthy time constants requiring considerable time to manifest. By optimizing specific gradient directions, it is possible to accelerate coaching simply by concentrating on a subset of eigenvectors and aligning their magnitude with that of other dominant components, an adjustment that can be implemented through a straightforward modification to either the loss function or the optimizer itself? We delve deeper into these possibilities by incorporating an extra dimension to our research.
The scientific underpinning of SSL enables a recursive inquiry into the properties of personal eigenmodes, facilitating a deeper exploration of their characteristics and implications. Is the discovery of new information more significant when it occurs early on in a process rather than being uncovered later on? The prevalence of distinct augmentation strategies in altering discovered modes hinges heavily on the specific SSL methodology employed. Can we systematically assign meaningful content to specific subsets of eigenmodes, enabling us to interpret their physical significance and utilize them more effectively in simulations? By observing the initial modes found, we’ve noticed that they often represent highly interpretable features, such as an image’s dominant color and saturation. If various types of illustration learning converge to similar representations – a hypothesis that can be empirically verified – then answers to these questions could have implications extending to deep learning more broadly?
With all thoughts oriented, we’re confident about the potential for future projects within this sphere. While deep learning remains an intriguing theoretical enigma, our research provides a solid foundation for future investigations into the training dynamics of deep networks.
